Главной физической величиной, характеризующей электрическое поле, является напряженность электрического поля.
Напряженность электрического поля есть векторная величина, равная пределу отношения силы ![]() , с которой электрическое поле действует на неподвижное точечное положительно заряженное тело, внесенное в рассматриваемую точку поля, к заряду этого тела q0, когда этот заряд стремится к нулю, и имеющая направление, совпадающее с направлением силы:
, с которой электрическое поле действует на неподвижное точечное положительно заряженное тело, внесенное в рассматриваемую точку поля, к заряду этого тела q0, когда этот заряд стремится к нулю, и имеющая направление, совпадающее с направлением силы:
![]() . (1.1)
. (1.1)
Единицей измерения напряженности поля является В/м.
Из выражения (1.1) следует, что сила ![]() , действующая на точечный заряд q конечной величины, внесенный в поле, будет равна:
, действующая на точечный заряд q конечной величины, внесенный в поле, будет равна:
![]() .
.
Если два точечных заряда q1 и q2 расположены в пустоте, то сила взаимодействия между ними, согласно опытному закону Кулона, равна:
![]() ,
,
где ![]() _ единичный вектор, направленный по линии, соединяющей заряды;
_ единичный вектор, направленный по линии, соединяющей заряды; ![]() = 8.85 · 10-12 Ф/м – электрическая постоянная; r – расстояние между зарядами, м.
= 8.85 · 10-12 Ф/м – электрическая постоянная; r – расстояние между зарядами, м.
Из закона Кулона следует выражение для напряженности электрического поля точечного заряда q, расположенного в пустоте:
![]() . (1.2)
. (1.2)
Здесь единичный вектор направлен от заряда q в точку наблюдения; r – расстояние от заряда до точки наблюдения.
При расчете электростатических полей важное значение имеет теорема Гаусса, которая в интегральной форме для пустоты имеет вид:
![]()
и гласит о том, что поток вектора напряженности электрического поля сквозь замкнутую поверхность s в пустоте равен отношению электрического заряда q, заключенного внутри этой поверхности, к электрической постоянной ![]() .
.
Если электрическое поле имеет место в диэлектрике, то наблюдается поляризация вещества и появляются связанные электрические заряды. Учитывают поляризацию с помощью
вектора поляризации ![]() , который для анизотропных и однородных сред выражается через напряженность поля следующим образом:
, который для анизотропных и однородных сред выражается через напряженность поля следующим образом: ![]() , где c – диэлектрическая восприимчивость вещества (диэлектрика). Вектор поляризации равен также поверхностной плотности связанных зарядов, возникающих в диэлектрике под воздействием внешнего электрического поля (Р = sсвяз). Кроме этого, при анализе электростатических полей используют вектор электрического смещения:
, где c – диэлектрическая восприимчивость вещества (диэлектрика). Вектор поляризации равен также поверхностной плотности связанных зарядов, возникающих в диэлектрике под воздействием внешнего электрического поля (Р = sсвяз). Кроме этого, при анализе электростатических полей используют вектор электрического смещения:
![]() .
.
Единицей электрического смещения является Кл/м2.
Величина e = e0 + c является основной характеристикой диэлектрика и называется абсолютной диэлектрической проницаемостью. Отношение er = e/e0 называют относительной диэлектрической проницаемостью.
Для однородного изотропного диэлектрика теорема Гаусса будет иметь в интегральной форме вид:
![]() .
.
Для любой среды справедливы обобщенная теорема Гаусса или постулат Максвелла:
![]() .
.
Теорема Гаусса и постулат Максвелла в дифференциальной форме записи имеют вид:
![]() .
.
или в иной форме:
![]() ,
,
где r – объемная плотность электрического заряда в данной точке пространства. Выражение, стоящее в левой части уравнения, называется расхождением или дивергенцией вектора напряженности или электрического смещения. Расхождение иногда обозначают через знак Ñ (читается «набла»), который называется символическим дифференциальным векторным оператором Гамильтона.
Для электростатического поля справедливо также уравнение
![]() (1.3)
(1.3)
или в дифференциальной форме
![]() , (1.4)
, (1.4)
где l – контур интегрирования. Величина, стоящая в левой части последнего уравнения, называется вихрем или ротором.
Условие (1.3) или (1.4) говорит о том, что в электростатическом поле линейный интеграл от вектора напряженности поля, взятый от любой точки А до любой точки В, не зависит от выбора пути интегрирования и полностью определяется в заданном поле положением точек А и В. Это обстоятельство позволяет ввести понятие о потенциале электростатического поля. Потенциал электростатического поля в точке А определяется как линейный интеграл вектора ![]() , взятый от точки А до некоторой точки Р:
, взятый от точки А до некоторой точки Р:
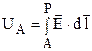 . (1.5)
. (1.5)
Потенциал в точке Р равен нулю.
Линейный интеграл вектора напряженности поля вдоль некоторого пути от точки А до точки В есть разность потенциалов в точках А и В:
![]() . (1.6)
. (1.6)
Электрический потенциал, с учетом условия (1.4), может быть связан с вектором напряженности электрического поля при помощи следующего соотношения:
![]() . (1.7)
. (1.7)
В однородной среде (e = const) для потенциала справедливо уравнение Пуассона:
Ñ2U = -r/e
и, в частности, при r = 0 уравнение Лапласа:
Ñ2U = 0.
Оператор Ñ2 часто обозначают ![]() и называют оператором Лапласа или лапласианом.
и называют оператором Лапласа или лапласианом.
В случае, когда среда неоднородна, при анализе электростатических полей используют граничные условия. Так, граница раздела диэлектрик-проводник является поверхностью равного электрического потенциала (U = const), и линии напряженности поля в диэлектрике нормальны к ней. Обозначив через Еn и Еt нормальную и касательную к поверхности проводника составляющие вектора напряженности поля в диэлектрике около поверхности проводника, указанные условия можно записать в виде:
Еt = 0; Е = Еn = -e·¶U/¶n = s,
где s – поверхностная плотность электрического заряда на поверхности проводника.
На поверхности раздела двух диэлектриков равны между собой касательные составляющие напряженности поля (Еt1 = Еt2) и нормальные составляющие вектора электрического смещения (Dn1 = Dn2).
Из данных граничных условий можно получить еще одно условие – условие преломления линий поля при переходе их из одного диэлектрика в другой:
![]() ,
,
где q1 и q2 – углы между вектором напряженности (или смещения) и нормалями к границе раздела сред.
При этом, если вектор напряженности перпендикулярен к границе раздела, то электрическое смещение не меняется при переходе из одной среды в другую, а напряженность поля меняется скачком.
Система заряженных тел является носителем определенного запаса энергии. Энергия электрического поля распределяется во всем объеме поля. При этом каждая точка поля характеризуется объемной плотностью энергии:
![]() .
.
Соответственно, энергия поля, запасенная в объеме V, может быть представлена следующим выражением:
![]() .
.
Единицей энергии является джоуль (Дж).
Энергия системы заряженных n тел определяется по формуле
![]() .
.
В частности, энергия конденсатора, который состоит из двух обкладок (тел), заряженных одинаковым по величине, но противоположным по знаку зарядом q, равна
![]() ,
,
где С – емкость конденсатора; u – разность потенциалов между обкладками.
Механические силы взаимодействия точечных заряженных тел могут быть вычислены при помощи закона Кулона. В случаях, когда заряженные тела нельзя рассматривать как точечные, непосредственное применение закона Кулона невозможно. Поэтому механические силы определяют исходя из энергетических соотношений:
![]() .
.
Здесь g – обобщенная координата.
Таким образом, механическая сила, стремящаяся изменить данную координату g системы, равна изменению энергии электрического поля, отнесенному к единице производимого силой изменения координаты в предположении, что либо заряды, либо потенциалы всех тел сохраняются неизменными.
Единицей силы является ньютон (Н).
В некоторых частных случаях сила определяется достаточно просто. Так, сила, действующая на заряженное тело, заряд которого распределен по объему с объемной плотностью r, равна:
![]() .
.
Сила, действующая на поверхность заряженного проводника, определяется при помощи формулы
![]() .
.
Плотность механической силы (давление) в любой точке поверхности этого проводника равна объемной плотности энергии электрического поля в этой же точке:
![]() .
.
Объемная плотность механической силы, действующей на диэлектрик, равна
![]()
и направлена в сторону максимального возрастания напряженности электрического поля.
Сила притяжения между обкладками конденсатора (при пренебрежении краевым эффектом) определяется следующим выражением:
![]() ,
,
где S – площадь обкладки.
Сила притяжения (на единицу длины) между параллельными цилиндрическими проводниками равных радиусов R, с расстоянием между осями d >> 2R и заряженных равными по величине и противоположными по знаку зарядами определяется формулой
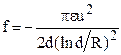 .
.
Здесь u – разность потенциалов между проводниками.
Электрическая емкость характеризует способность тела или системы тел накапливать электрические заряды, запасая, таким образом, энергию электрического поля.
Емкость определяют как отношение заряда уединенного проводящего тела к его потенциалу: С = q/U, а емкость двух проводящих тел, разделенных диэлектриком и заряженных равными по значению и противоположными по знаку зарядами, – как отношение абсолютного значения заряда к разности потенциалов этих тел: С = q/(U1 – U2).
Емкость зависит от геометрических размеров, конфигурации, диэлектрической проницаемости диэлектрика и взаимного расположения тел.
Емкость измеряется в фарадах (Ф).
Ниже приведены выражения для емкостей простейших систем.
Емкость плоского конденсатора с однослойным диэлектриком равна:
С = (eS)/d,
где S – площадь каждой пластины; d – расстояние между пластинами.
Емкость плоского конденсатора с двухслойным диэлектриком с диэлектрической проницаемостью e1 и e2 каждого слоя и их толщиной, равной d1 и d2, определяется выражением:
![]() .
.
Емкость на единицу длины цилиндрического конденсатора (коаксиального кабеля) с однослойным диэлектриком и радиусами обкладок R1 и R2 (R1 < R2):
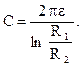
Емкость сферического конденсатора с наружным радиусом внутренней сферической обкладки R1 и внутренним радиусом внешней сферической обкладки R2 определяется выражением:
![]() .
.
Емкость уединенного шара радиусом R равна:
С = 4peR. (1.8)
Емкость двух шаров радиусами R1 и R2, расположенных на расстоянии D:
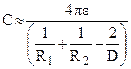 .
.
Емкость уединенного цилиндра радиусом R и длиной l:
 .
.
Если длина цилиндра много больше его радиуса (l>>R), то емкость можно определять по приближенной формуле
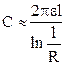 .
.
Емкость двухпроводной линии с учетом влияния земли:
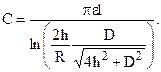 (1.9)
(1.9)
Здесь h – высота подвеса параллельных проводов над землей; R – радиус провода; D – расстояние между проводами; l – длина проводов.
Если высота подвеса много больше расстояния между проводами, то
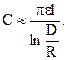
Емкость трехфазной линии передачи с учетом влияния земли при параллельном расположении проводов:
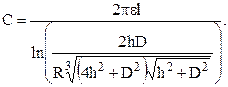 (1.10)
(1.10)
При высоте подвеса h много больше расстояния между проводами D емкость трехфазной линии равна:
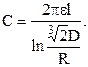
При наличии нескольких заряженных проводников вводят понятие частичных емкостей и эквивалентной емкости системы.
Частичной емкостью называется емкость между двумя проводниками, входящими в систему проводников. Частичную емкость между двумя проводниками определяют как абсолютное отношение заряда одного проводника к разности потенциалов между этими проводниками, когда остальные проводники системы имеют один и тот же потенциал.
Эквивалентная емкость (рабочая) – емкость между двумя проводниками, входящими в систему проводников, учитывающая частичные емкости между парой проводов системы.
Рассмотрим несколько примеров по расчету электрического поля с использованием вышеприведенных выражений.
Пример 1.1. Точечный заряд q = 10-9 Кл помещен в начале сферической системы координат. Определить напряжение между точками а (Ra = 4 см, qа = 45º, jа = 0º) и b (Rb = 8 см, qb = 180º, jb = 90º) и напряженность в тех же точках, если окружающей средой является воздух.
Решение будем проводить с помощью теоремы Гаусса, так как среда однородна.
Поскольку поле точечного заряда характеризуется сферической симметрией, то, если в качестве поверхности интегрирования взять поверхность сферы с центром в точке, где расположен заряд (в нашем случае это начало системы координат), то в любой точке на поверхности этой сферы напряженность поля будет иметь одно и то же значение. Направление же вектора ![]() будет совпадать с направлением радиуса, то есть перпендикулярно к поверхности сферы. В связи с этим интеграл по этой поверхности, составленный по теореме Гаусса, можно преобразовать следующим образом:
будет совпадать с направлением радиуса, то есть перпендикулярно к поверхности сферы. В связи с этим интеграл по этой поверхности, составленный по теореме Гаусса, можно преобразовать следующим образом:
![]() .
.
Поскольку данный интеграл (согласно теореме Гаусса) равен отношению заряда, помещенного внутри сферы, к диэлектрической проницаемости среды, то напряженность поля будет определяться соотношением
Еr = q/(4pe0r2).
Здесь индекс r у напряженности проставлен для того, чтобы показать, что напряженность поля имеет одну составляющую, направленную по радиусу.
Отметим, что данная формула полностью соответствует выражению (1.2), полученному из закона Кулона.
Поскольку напряженность электрического поля в данном случае имеет только радиальную составляющую, величина которой является функцией радиуса и не зависит от угловой координаты, то в указанных в исходном задании точках она будет равна:
E(ra) = q/(4pe0ra2) = 10-9/(4p · 8.85 · 10-12 · 0.042) = 5.62 кВ/м.
E(rb) = q/(4pe0rb2) = 10-9/(4p · 8.85 · 10-12 · 0.082) = 1.405 кВ/м.
Разность потенциалов между точками а и b определяется при помощи выражения (1.6). Эта разность в потенциальном поле не зависит от пути интегрирования. Поэтому, если разбить путь интегрирования на две части и вначале проводить интегрирование вдоль радиуса от точки а до точки, которая является точкой пересечения продолжения этого радиуса с поверхностью воображаемой сферы с центром в начале координат и радиусом rb, а затем проводить интегрирование по любой линии, лежащей на поверхности этой сферы от данной точки до точки b, то интеграл вдоль этой линии будет равен нулю, поскольку вектор напряженности поля имеет одну составляющую, направленную вдоль радиуса, а подынтегральным выражением в формуле (1.6) является скалярное произведение вектора напряженности поля и вектора dl, который совпадает с касательной к поверхности сферы.
Таким образом, разность потенциалов между точками а и b будет равна
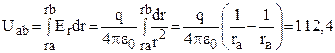 В.
В.
Пример 1.2. Уединенный проводящий шар радиусом R0 = 6 см, поверхностная плотность заряда которого s = 0.1·10-6 Кл/м2, помещен в диэлектрик (er = 3). Определить закон изменения напряженности поля и потенциала в функции расстояния r от центра шара, приняв потенциал равным нулю в бесконечности. Рассчитать напряжение между точками, одна из которых лежит на поверхности шара, а другая – на расстоянии 20 см от его поверхности. Вычислить емкость шара.
Поле внутри проводящего шара отсутствует. Поле вне шара обладает сферической симметрией, поэтому рассчитывается с помощью теоремы Гаусса точно так же, как и для точечного заряда:
![]()
Здесь в качестве поверхности интегрирования взята поверхность сферы радиуса r ³ R0 с центром, совпадающим с центром шара.
Заряд шара определяется через поверхностную плотность:
q = s·4p·R02.
Таким образом, напряженность поля вне шара имеет только одну радиальную составляющую и равна
Еr = s·R02/(ere0r2) = 0.1·10-6·0.062/(3·8.85·10-12 · r2).
Потенциал в любой точке вне шара, находящейся на расстоянии r от его центра, определяется с помощью выражения (1.5), которое с учетом того, что напряженность поля направлена вдоль радиуса, будет иметь следующий вид:
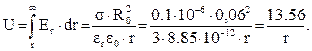
Потенциал шара равен потенциалу любой точки, лежащей на поверхности шара (r = R0), U = 13.56/0.06 = 173.8 В.
Разность потенциалов между любыми точками А (r = RA) и В (r = RВ) определяется с помощью следующей формулы
UA – UВ = 13.56 · (1/RA – 1/RВ).
Таким образом, разность потенциалов между точкой, лежащей на поверхности шара, и точкой, отстоящей от поверхности на расстоянии 20 см, равна
UAВ = 13.56 · (1/0.06 – 1/0.26) = 173.8 В.
Емкость шара можно определять выражением (1.8):
С = 4·p·ere0·R0 = 4·p·3 · 8.85 · 10-12 · 0.06 = 2 · 10-11 Ф.
Пример 1.3. Шар из диэлектрика (er = 4) заряжен и расположен в воздухе. Объемная плотность заряда является функцией расстояния r от центра шара: r = k·r, где k = 0,05p [Кл/м4]. Радиус шара R = 2 см. Рассчитать и построить графики изменения потенциала и напряженности поля вдоль радиуса.
В данном случае поле также обладает сферической симметрией, но область не однородна. Поэтому здесь удобнее применять постулат Максвелла.
Так, при 0 £ r £ R
![]()
где s – сферическая поверхность радиусом r с центром, совпадающим с центром шара; v – объем, заключенный внутри этой поверхности.
Перепишем уравнение с учетом симметрии поля:
![]()
Отсюда находим радиальную составляющую вектора электрического смещения:
Dr = 0.25·k·r2.
Напряженность электрического поля, которая так же, как и вектор электрического смещения, направлена по радиусу, внутри шара будет равна:
E1r = Dr/ere0 = 0.25·k·r2/ere0.
Вне шара (r ³ R) электрическое смещение, исходя из постулата Максвелла, определяется следующим образом:
![]()
Следовательно, электрическое смещение и напряженность поля будут равны:
Dr = 0.25·k·R4/r2; Er = Dr/e0.
Графики изменения напряженности поля и вектора электрического смещения представлены на рис. 1.1. Значения напряженности поля и вектора электрического смещения даны в относительных единицах. За базисные значения приняты значения этих величин на поверхности шара, которые для заданных исходных данных соответственно равны:
Erb = 4.435·105 В/м; Drb = 1.571·10-5 Кл/м2.
Потенциал поля внутри шара можно определить по формуле
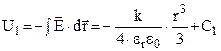 ,
,
где С1 – постоянная интегрирования.
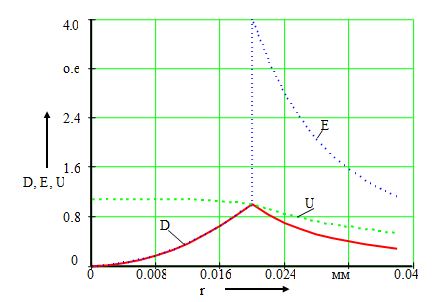
Рис. 1.1. Графики изменения напряженности
Принимая потенциал бесконечно удаленной точки равным нулю, определим потенциал любой произвольной точки в области вне шара:
 .
.
Постоянную интегрирования С1 можно определить из условия равенства потенциалов U1 и U2 на поверхности шара (при r = R)
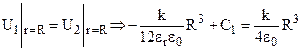 .
.
Отсюда
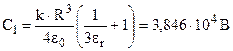 .
.
Отметим, что если бы объемная плотность заряда r оставалась постоянной, то напряженность поля и потенциалы поля в соответствующих подобластях определялись бы следующими выражениями:
E1 = r·r/(3·ere0); U1 = — r·r2/(6·ere0) + C1;
E2 = r·R3/(3·e0·r2); U2 = r·R3/(3·e0·r).
Постоянная С1 в этом случае определяется также из условия равенства потенциалов U1 и U2 на поверхности шара
С1 = r·R3· (1 + 2·er)/(6·e0·er).
Пример 1.4. Бесконечно длинная тонкая заряженная нить расположена в воздухе вдоль оси z цилиндрической системы координат (рис. 1.2). Линейная плотность заряда t = 10-9 Кл/м. Рассчитать и построить график изменения напряженности поля вдоль радиуса. Определить разность потенциалов между точками m (rm = 10 cм; qm = 270º) и n (rn = 40 cм; qn = 180º).
Рис. 1.2. Бесконечно длинная нить
В этом случае поле характеризуется цилиндрической симметрией, то есть во всех точках цилиндрической поверхности, охватывающей заряженную нить, произвольного радиуса r напряженность поля имеет одно и то же значение и направлена перпендикулярно к поверхности. Поэтому, если окружить нить цилиндрической поверхностью длиной l и радиусом r и использовать теорему Гаусса, то можно получить выражение для напряженности поля Е:
![]()
График изменения напряженности поля вдоль радиуса представлен на рис. 1.3.
Значение напряженности поля на графике дано в относительных единицах. За базисное значение принято значение напряженности на расстоянии одного миллиметра от начала координат (Еb = 1,798·104 В/м).
Потенциал поля в любой точке m, расположенной на расстоянии rm от оси провода, равен:
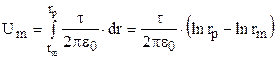 .
.
Здесь rp – расстояние от оси провода до некоторой фиксированной точки пространства р, в которой потенциал принимается равным нулю.
Если за такую точку принять точку, расположенную на расстоянии одного метра от оси провода, то потенциал точки m будет равен:
![]() .
.
Изменение потенциала вдоль радиуса представлено на рис. 1.3. Значения потенциала даны также в относительных единицах. За базисное значение потенциала принято значение потенциала в той же точке, что и базисное значение напряженности поля (Ub = 124.226 В).
Разность потенциалов между точками, указанными в условии задачи, равна 24.931 В.
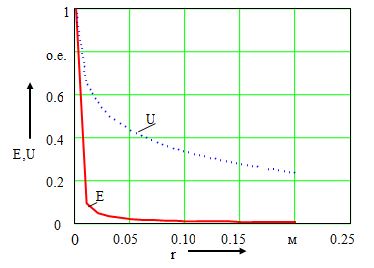
Рис. 1.3. Изменение потенциала
Пример 1.5. Рассчитать электростатическое поле от двух бесконечно длинных, равномерно заряженных, параллельных, тонких проводников, расположенных в воздухе на расстоянии 2d = 6 м друг от друга. Проводники имеют одинаковые по величине, но противоположные по знаку заряды, линейная плотность которых равна t = 4·10-9 Кл/м.
Построить график изменения напряженности поля вдоль оси Y (при х = 0) и вывести уравнения для построения эквипотенциальных линий и линий поля.
Поскольку среда линейна, то данную задачу можно решить методом наложения. Вначале рассчитываем напряженность поля в любой точке М от правого провода (рис. 1.4), а затем в этой же точке от левого провода.
Задача по расчету поля от бесконечно длинного заряженного провода решена в примере 1.4. Поэтому сразу запишем выражения для определения напряженности поля от правого и левого провода:
![]()
Направление векторов напряженности поля показано на рис. 1.4.
Результирующая напряженность поля определяется как векторная сумма этих векторов:
![]() .
.
Модуль данной результирующей напряженности поля рассчитывается по формуле
![]()
где E1x, E2x, E1y, E2y – проекции векторов напряженности поля на соответствующие декартовы оси координат:
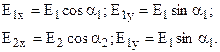
Здесь ![]() yм и xм – координаты произвольной точки М.
yм и xм – координаты произвольной точки М.
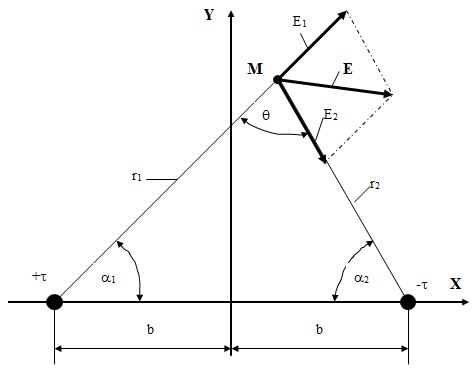
Рис. 1.4. Направление векторов напряженности поля
В частности, если точка М лежит на оси Y, то (r1 = r2) результирующая напряженность поля будет направлена вдоль оси Х (Е = Ех). График распределения данной величины вдоль оси Y представлен на рис. 1.5. Значения напряженности поля на графике даны в относительных единицах, при этом за базисное значение принято значение напряженности в начале координат (x = 0, y = 0), которое оказалось равным 47.956 В/м.
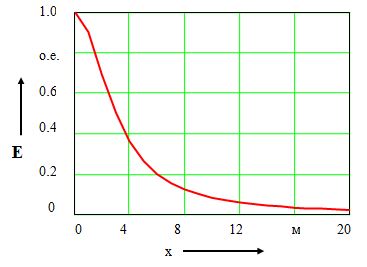
Рис. 1.5. График распределения данной величины
Потенциал поля в любой точке М определяется так же как сумма потенциалов поля от одного и другого провода:
![]()
Здесь С – постоянная интегрирования. Эта постоянная будет равна нулю, если принять потенциал точки, которая находится в начале координат, равным нулю.
В этом случае ось OY будет являться эквипотенциальной линией нулевого потенциала.
Все остальные линии равного потенциала являются окружностями с центрами, лежащими на оси ОХ. Координаты этих центров и радиусы окружностей определяются с помощью следующих формул:
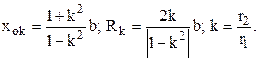
Таким образом, если необходимо провести линию равного потенциала через точку, потенциал которой задан (например, 100 В), то надо определить k, используя формулу для потенциала:
![]()
При построении картины поля, для того чтобы приращение потенциала при переходе от любой линии равного потенциала к соседней оставалось постоянным, должно соблюдаться условие
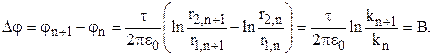
Здесь В – постоянная; n – порядковый номер линии равного потенциала.
Таким образом, число k при возрастании порядкового номера линии равного потенциала n должно изменяться в геометрической прогрессии.
Линиями поля данной системы заряженных проводников являются дуги окружностей, пересекающихся с проводниками. При этом центры этих дуг лежат на оси OY и имеют координаты, которые определяются при помощи следующей формулы:
![]()
Чтобы при построении картины поля подразделить поле на трубки равного потенциала, необходимо при переходе от любой линии напряженности поля к соседней изменять угол J на постоянную величину.
Пример 1.6. Два одинаковых бесконечно длинных проводящих цилиндра расположены в воздухе. Радиус цилиндров R = 0.04 м, расстояние между геометрическими осями 2h = 0.12 м (рис. 1.6).
Напряжение, приложенное к цилиндрам U12 = 100 В.
Рассчитать электростатическое поле, построить графики изменения напряженности поля и потенциала вдоль оси х. Найти емкость системы проводов на единицу длины.
Поле внутри проводящих проводов отсутствует. Поле же в воздухе будет точно таким, как и поле от двух бесконечно тонких линейных проводников, проходящих через электрические оси данных проводов.
Таким образом, задача по расчету поля двух проводов круглого сечения сводится к нахождению электрических осей проводов, поскольку в дальнейшем расчет поля в воздухе будет аналогичным расчету поля, проведенному в предыдущем примере.
Поскольку поверхность проводящих проводов является поверхностью равного потенциала, то, используя выражения для координаты центра и радиуса линий равного потенциала, которые приведены в примере 1.5, можно получить формулу для определения координат центра электрических осей проводов b:
![]()

Рис. 1.6. Два одинаковых бесконечно длинных проводящих цилиндра
В условии задачи задана не линейная плотность зарядов, а разность потенциалов между проводами (разность потенциалов между точками m и n). Поэтому, прежде всего, следует определить линейную плотность зарядов t. Для этого используем выражение для потенциалов, которое также приведено в предыдущем примере
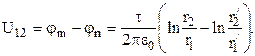
Здесь r1 и r2 – расстояние от электрической оси первого (левого) и второго провода, соответственно, до точки m, которая находится на поверхности первого провода, а r1/ и r2/ – расстояние от электрической оси первого и второго провода, соответственно, до точки n, которая находится на поверхности второго провода:
![]()
С учетом последних соотношений можно записать выражение для определения линейной плотности зарядов:
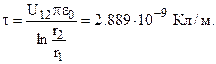
После определения линейной плотности зарядов и расположения электрических осей проводов, выражения для расчета напряженности поля и потенциала в области вне проводов полностью аналогичны тем, которые приведены в примере 1.5.
Графики распределения напряженности поля и потенциала вдоль оси ОХ (при y = 0) приведены на рис. 1.7. Все значения на графике даны в относительных единицах, причем, за базисные значения приняты значения напряженности поля и потенциала на поверхности правого провода, которые оказались равными Еб = 2904 В/м, jб = -50 В.
С учетом того, что ось OY является осью симметрии для напряженности поля и осью антисимметрии для потенциала, графики построены только для положительных значений х.
Емкость между двумя проводниками на единицу их длины определяется при помощи следующего выражения:
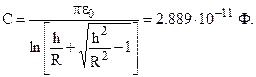
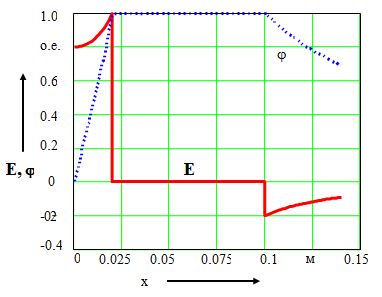
Рис. 1.7. Графики распределения напряженности поля и потенциала