Случайной величиной называют такую величину, значения которой изменяются при повторении опытов некоторым, заранее не предсказуемым образом. Для случайной величины нельзя заранее точно сказать, какое конкретное значение она примет в данном опыте, но можно указать закон ее распределения. Закон распределения считается заданным, если:
1) указано множество возможных значений случайной величины;
2) указан способ определения вероятности попадания случайной величины в любую область множества возможных значений.
Вероятность попадания в заданную область может быть определена следующим образом:
Здесь Nm – количество наблюдений случайной величины, оказавшихся в заданной области; N – общее количество наблюдений.
Аналитическими выражениями закона распределения случайной величины являются функции распределения вероятностей – интегральная и дифференциальная.
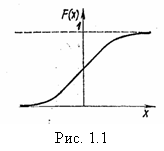
Интегральная функция распределения F(x) случайной величины X показывает вероятность того, что случайная величина не превышает некоторого заданного или текущего значения x, т.е.
Следовательно, вероятность того, что значение случайной величины Х заключено между 
и
, равна разности значений функции распределения, вычисленных в этих двух точках:
а также
Интегральная функция обладает следующими свойствами:
1) 
;
2) 
;
3) 
для всех х;
4) 
, если 
.
Вид функции распределения F(x) изображен на рис. 1.1.
Если функция F(x) дифференцируема для всех значений случайной величины Х, то закон распределения вероятностей может быть выражен в аналитической форме также с помощью дифференциальной функции распределения вероятностей:
.
Таким образом, значение функции f(x) приближенно равно отношению вероятности попадания случайной величины в интервал 
к длине (
) этого интервала, когда – бесконечно малая величина. Поэтому функцию f(x) называют также функцией плотности распределения вероятностей.
Основные свойства функции f(x):
1) 
; 2) 
;
3) 
; 4) 
(z – переменная интегрирования).
С помощью дифференциальной функции распределения вычисляется вероятность нахождения случайной величины в любой области из множества ее возможных значений. В частности,
, 
, 
.
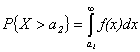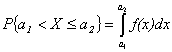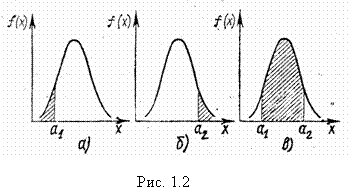
Для непрерывной случайной величины вероятность можно определить как относительную долю площади под кривой плотности распределения вероятностей f(x). Так, например, вероятность того, что случайная величина Х примет значение:
1) меньшее 
, равна относительной доле площади под кривой f(x) слева от точки (рис. 1.2, а);
2) большее 
, равна относительной доле площади под кривой f(x) справа от точки (рис. 1.2, б);
3) заключенное между и , равна относительной доле площади под кривой f(x) между точками и (рис. 1.2, в).
Как интегральная, так и дифференциальная функции распределения являются исчерпывающими вероятностными характеристиками случайной величины. Однако некоторые основные свойства случайных величин могут быть описаны более просто, с помощью определенных числовых параметров.
Наиболее часто на практике используются два параметра, характеризующие центр рассеяния (центр распределения) случайной величины и степень ее рассеяния вокруг этого центра. Наиболее распространенной характеристикой центра распределения является математическое ожидание (mх) случайной величины Х, часто называемое также генеральным средним значением:
.
Степень рассеяния случайной величины Х относительно mx может быть охарактеризована с помощью генеральной дисперсии 
:
.
Если f(x) все в большей степени концентрируется вблизи mx, то значения уменьшаются. Если же имеются весьма удаленные от mx значения случайной величины Х и для них f(x) не слишком мала, то дисперсия увеличивается. Квадратный корень из дисперсии () называется средним квадратическим отклонением (
).
Зачастую для описания практической ситуации оказывается необходимым использование одновременно нескольких (в простейшем случае – двух) случайных величин. Для задания вероятностных свойств двух случайных величин X, Y используются двумерные (совместные) функции распределения вероятностей: интегральная F(x,y) и дифференциальная f(x,y).
Функция F(x,y), характеризующая вероятность того, что первая случайная величина принимает некоторое значение, меньшее или равное х, а вторая – значение, меньшее или равное y, называется интегральной функцией совместного распределения двух случайных величин:
.
Как и для одной непрерывной случайной величины, если функция F(x,y) достаточно гладкая, то ее можно продифференцировать, в результате чего получится двумерная дифференциальная функция распределения вероятностей (двумерная плотность вероятности):
.
Функция f(x, y)обладает следующими свойствами:
1) 
;
2) 
;
3) 
;
4) 
.
(
и 
– переменные интегрирования).
Вероятность того, что случайные величины X, Y одновременно попадут в некоторую произвольную область 
, составляет:
.
В частности,
.
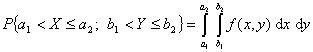По известной двумерной плотности f(x,y) легко найти частные (одномерные) функции распределения f(x), f(y) каждой случайной величины:
, 
.
Две случайные величины X и Y называются независимыми, если
.
Как и в одномерном случае, основные свойства двумерной совокупности величин X, Y могут быть охарактеризованы с помощью ряда числовых параметров. При этом в качестве наиболее употребительных параметров, описывающих поведение каждой из случайных величин в отдельности, используются математическое ожидание и дисперсия соответствующей случайной величины: mx, my, 
, 
.
Кроме параметров для двумерной совокупности могут быть использованы параметры, характеризующие степень взаимозависимости переменных X и Y. Простейшими из них являются:
1) ковариация двух случайных величин (называемая также корреляционным моментом):
,
2) а также нормированный показатель связи – коэффициент корреляции
.
По своему физическому смыслу коэффициент корреляции является далеко не исчерпывающей характеристикой статистической связи линейной зависимости между Х и Y. Коэффициент корреляции меняется в пределах 
:
· если 
, то случайные величины полностью положительно коррелированны, т.е. 
, где 
– постоянные, причем 
:
· если же 
, то случайные величины полностью отрицательно коррелированны, т.е. 
;
· если 
, то говорят, что случайные величины Х и Y не коррелированны: 
.
В том случае, когда Х и Y – независимые случайные величины, для них ; следовательно, они и не коррелированны. Обратное утверждение в общем случае неверно: Х и Y могут быть связаны функционально, но все же иметь нулевой коэффициент корреляции (при этом, конечно, функциональная связь должна быть нелинейной).
Все описанные функции и связанные с ними параметры являются теоретическими, характеризующими определенные свойства изучаемого объекта. На практике почти
всегда эти характеристики неизвестны, и возникает задача экспериментального (эмпирического) определения тех или иных характеристик случайных величин на основе наблюдений.