Удобное выражение для элемента площади ![]() получим, введя прямоугольную сетку. Разобьём объём D на части прямыми, параллельными осям координат x = const и y = const (рис. 1.6). Тогда
получим, введя прямоугольную сетку. Разобьём объём D на части прямыми, параллельными осям координат x = const и y = const (рис. 1.6). Тогда
![]() , (1.47)
, (1.47)
и двойной интеграл записывается ещё так:
![]() . (1.48)
. (1.48)
 Для дальнейшего предположим, что область D имеет такое устройство: она ограничена графиками функций
Для дальнейшего предположим, что область D имеет такое устройство: она ограничена графиками функций ![]() и
и ![]() и прямыми x = a и x = b (рис. 1.7). Каждая прямая, параллельная оси Оy (кроме прямы x = a и x = b) (рис. 1.8.) пересекает границу области D в двух точках. Нижнюю из этих точек будем называть точкой входа, а верхнюю – точкой выхода. Если D имеет другую конструкцию, то её разбивают и сводят к конструкции области D и далее используют свойство аддитивности интеграла.
и прямыми x = a и x = b (рис. 1.7). Каждая прямая, параллельная оси Оy (кроме прямы x = a и x = b) (рис. 1.8.) пересекает границу области D в двух точках. Нижнюю из этих точек будем называть точкой входа, а верхнюю – точкой выхода. Если D имеет другую конструкцию, то её разбивают и сводят к конструкции области D и далее используют свойство аддитивности интеграла.
Чтобы вычислить (1.48) интерпретируем его как массу М пластинки D. Найдем массу этой же пластинки иначе.
Рассмотрим узкий вертикальный стержень между прямыми х и x + dx (рис. 1.7) оси Ох.
Выделим элемент длиной dy стержня. Его площадь есть dxdy, тогда масса его будет приближенно равна f(x, y)dxdy. Чтобы найти массу всего стержня надо «просуммировать» массы всех элементов dy, т.е. в пределе проинтегрировать по у:
![]() (dx – постоянно). (1.49)
(dx – постоянно). (1.49)
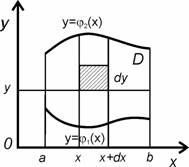
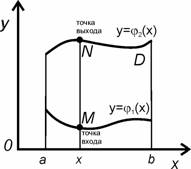
Рис. 1.7 Рис. 1.8
Чтобы получить массу всей пластинки D надо «просуммировать» массы всех бесконечно узких вертикальных стержней, т.е. проинтегрировать выражение (1.49) по х в пределах его изменения от a до b, получим:
![]() . (1.50)
. (1.50)
Так как эта же масса выражается двойным интегралом (1/36), то
![]() . (1.51)
. (1.51)
Методическое руководство
Чтобы вычислить двойной интеграл, надо проинтегрировать f(x,y) по у, считая х – фиксированным, в пределах от точки входа до точки выхода, а затем полученный результат проинтегрировать по х в пределах его наибольшего изменения.
Следовательно, для вычисления двойного интеграла нужно произвести последовательное вычисление двух обычных определенных интегралов. Интеграл
![]() ,
,
вычисляется первым, называется внутренним, а интеграл
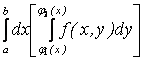
называется внешним.
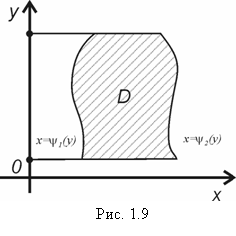 Если область D такая, как показано на рис. 1.9, то внутренне интегрирование удобно вести по х. Получается операция, которая носит название: изменения порядка интегрирования
Если область D такая, как показано на рис. 1.9, то внутренне интегрирование удобно вести по х. Получается операция, которая носит название: изменения порядка интегрирования
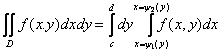 . (1.52)
. (1.52)
Формула (1.52) доказывается точно так же как и (1.51). Поскольку речь идет о массе одной и той же пластинки D, то
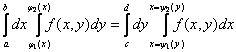 . (1.53)
. (1.53)
Методическое руководство
На практике трудность вычисления двойного интеграла обычно состоит в расстановке пределов. Следует руководствоваться следующей последовательностью действий:
1) сделать схематический рисунок области D, записав уравнения линий;
2) выбрать вполне определенный порядок интегрирования;
3) найти пределы для внешнего интеграла и расставить их;
4) произвольно (но не на концах отрезка) взять переменную между пределами внешнего интеграла и через эту точку провести прямую MN «входа-выхода»;
5) приступить к расстановке пределов для внутреннего интеграла: точка входа всегда лежит на кривой с определенным уравнением, с момента которой изменяется переменная интегрирования для внутреннего интеграла, точка выхода – на кривой, на которой заканчивается её изменение в области D, поэтому нижним пределом будет значение функции, на которой лежит точка входа; верхним – значение функции на которой лежит точка выхода.
Пример 1
Найти ![]() , где D:
, где D: ![]() .
.
Решение: Используя методическое руководство, выберем определенный порядок интегрирования и расставим пределы интегрирования:
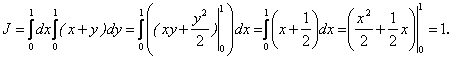
 Пример 2
Пример 2
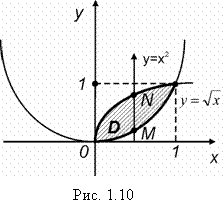
Найти площадь, ограниченную параболами y = x2 и ![]() (рис. 1.10).
(рис. 1.10).
Решение. По свойству (1.44)
![]() .
.
Для расстановки пределов необходимо решить систему:
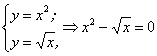 .
.
Отсюда: x1 = 0; х2 = 1, тогда
![]()
Пример 3
Изменить порядок интегрирования:
![]() .
.
Решение. Рекомендуется по заданным пределам во внешнем и внутреннем интегралах воспроизвести область интегрирования D: x = 0 и x = 1; y =x2 и y = x (рис. 1.11).
Поэтому
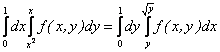 .
.
Пример 4
Вычислить объем тела, ограниченного поверхностями: z = x2 + y2, x = 0, x = 1 ; y = 0, y = (рис. 1.12).
Решение. Воспользуемся формулой (1.41):
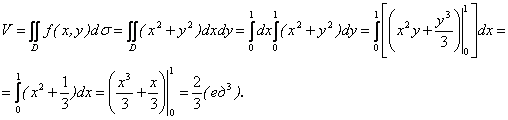
 Пример 5
Пример 5
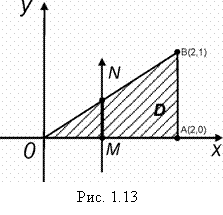
Вычислить ![]() , D – треугольник с вершинами О(0,0), A(2,0) и B(2,1) (рис. 1.13).
, D – треугольник с вершинами О(0,0), A(2,0) и B(2,1) (рис. 1.13).
Решение. Область D ограничена прямыми y = 0, ![]() , x =2. Тогда
, x =2. Тогда
