Для удобства вычислений вводят полярные координаты: x = rcosφ; y = rsinφ. Пусть область D ограничена двумя кривыми с полярными уравнениями r = r1(φ) и r = r2(φ) и лучами φ =φ1 и φ = φ2, исходящими из полюса (рис. 1.14). Требуется вычислить
![]() .
.
Используя связь декартовых координат с полярными, преобразуем функцию f(x, y) в функцию переменных r и φ:
![]()
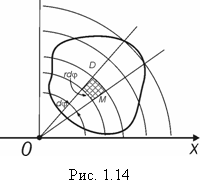 Найдем выражение для элемента площади в полярных координатах. Для чего разобьем область D с помощью окружностей
Найдем выражение для элемента площади в полярных координатах. Для чего разобьем область D с помощью окружностей ![]() и лучей
и лучей ![]() .
.
Получившийся элемент площади (рис. 1.14) можно принять за прямоугольник со сторонами ![]() и
и ![]() , тогда
, тогда
![]() (1.54)
(1.54)
дает выражение элемента площади в полярных координатах. Двойной интеграл примет вид:
![]() (1.55)
(1.55)
Чтобы вычислить этот интеграл, будем трактовать его как массу пластинки D с плотностью ![]() . Проведя разбиение так, как показано на (рис. 1.14) мы определим массу стрежня между лучами
. Проведя разбиение так, как показано на (рис. 1.14) мы определим массу стрежня между лучами ![]() и
и ![]() , после чего просуммируем все такие массы, т.е. проинтегрируем в пределах
, после чего просуммируем все такие массы, т.е. проинтегрируем в пределах ![]() до
до ![]() , получим массу всей пластины D. Итак,
, получим массу всей пластины D. Итак,
1) масса заштрихованного «прямоугольника» есть ![]() ;
;
 2)
2) ![]() – масса стержня (
– масса стержня (![]() и
и ![]() – постоянны);
– постоянны);
3) масса всей пластины равна:
![]() (1.56)
(1.56)
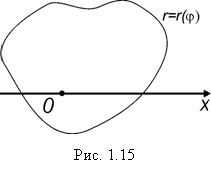
Если область D ограничена замкнутой кривой ![]() , а полюс лежит внутри области, то пределы будут (рис. 1.15):
, а полюс лежит внутри области, то пределы будут (рис. 1.15):
![]() (1.57)
(1.57)
 Пример 1
Пример 1
Вычислить ![]() , D – первая четверть круга радиуса R = 1, с центром в точке О(0,0).
, D – первая четверть круга радиуса R = 1, с центром в точке О(0,0).
Решение. Так как ![]() , а
, а ![]() . На основании формулы (1.56) имеем:
. На основании формулы (1.56) имеем:
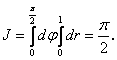
Пример 2
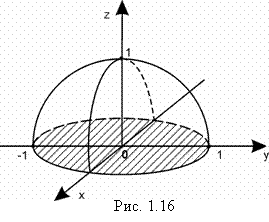
Найти объем V тела, ограниченного поверхностями ![]() и z= 0. (рис. 1.16).
и z= 0. (рис. 1.16).
Решение. Согласно (1.41.) ![]() , где D – круг
, где D – круг ![]() .
.
Перейдя к полярным координатам, получим:
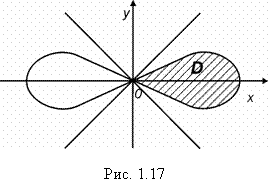
![]() ,
,
поэтому
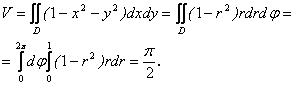
Пример 3
Найти площадь, ограниченную лемнискатой Бернулли:
![]() .
.
Решение. В полярной системе это уравнение имеет вид: ![]() (рис. 1.17).
(рис. 1.17).
Правая петля получена при изменении ![]() в пределах
в пределах ![]() , а левая при
, а левая при ![]() .
.
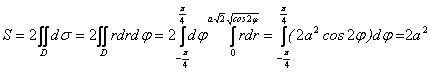 .
.