Пусть имеется набор (выборка) экспериментальных данных: ![]() ,
, ![]() , …,
, …, ![]() . Обработку этих данных для получения эмпирических характеристик одномерной случайной величины производят обычно в такой последовательности:
. Обработку этих данных для получения эмпирических характеристик одномерной случайной величины производят обычно в такой последовательности:
1) построение вариационного ряда;
2) построение диаграммы накопленных частот;
3) построение гистограммы выборки;
4) определение статистических оценок выборки;
5) проверка близости выборки к нормальному распределению случайной величины.
1. Построение вариационного ряда. Вариационный ряд ![]() ,
, ![]() , …,
, …, ![]() получают из исходных данных
получают из исходных данных ![]() путем их расположения в порядке возрастания от
путем их расположения в порядке возрастания от ![]() до
до ![]() так, чтобы
так, чтобы ![]() .
.
Пример 1
Имеется ряд данных х1 = 5, х2 = 3, х3 = 4; ![]() . Тогда им соответствует вариационный ряд:
. Тогда им соответствует вариационный ряд:
![]()
![]() ;
; ![]() ;
; ![]() .
.
2. Построение диаграммы накопленных частот ![]() , являющейся эмпирическим аналогом интегрального закона распределения. Диаграмму строят, вычисляя сумму накопленных частот по формуле:
, являющейся эмпирическим аналогом интегрального закона распределения. Диаграмму строят, вычисляя сумму накопленных частот по формуле:
![]() ,
,
 где
где ![]() – число элементов в выборке, для которых
– число элементов в выборке, для которых ![]() . Практически это делается так. На оси абсцисс указывают значение наблюдений
. Практически это делается так. На оси абсцисс указывают значение наблюдений ![]() . Значение
. Значение ![]() по оси ординат равно нулю левее точки
по оси ординат равно нулю левее точки ![]() ; в точке
; в точке ![]() и далее во всех других точках
и далее во всех других точках ![]()
![]() имеет скачок, равный 1/N. Если существует несколько совпадающих значений
имеет скачок, равный 1/N. Если существует несколько совпадающих значений ![]() , то в этом месте на диаграмме происходит скачок, равный
, то в этом месте на диаграмме происходит скачок, равный ![]() , где λ – число совпадающих точек. Ясно, что при
, где λ – число совпадающих точек. Ясно, что при ![]()
![]() = 1.
= 1.
Отметим, что если ![]() , то
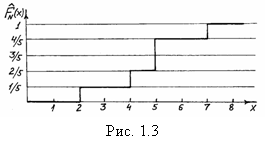
, то ![]() . Используя данные примера 1, построим соответствующую диаграмму (рис. 1.3).
. Используя данные примера 1, построим соответствующую диаграмму (рис. 1.3).
3. Построение гистограммы выборки. Гистограмма ![]() является эмпирическим аналогом функции плотности распределения f(x). Обычно ее строят следующим образом.
является эмпирическим аналогом функции плотности распределения f(x). Обычно ее строят следующим образом.
1) Находят предварительное количество квантов (интервалов), на которое должна быть разбита ось Ох. Это количество (К) определяют с помощью оценочной формулы:
![]() , (1.1)
, (1.1)
где найденное значение округляют до ближайшего целого числа.
2) Определяют длину интервала:
![]() . (1.2)
. (1.2)
Значение ![]() можно округлить для удобства вычислений до целого числа.
можно округлить для удобства вычислений до целого числа.
3) Середину области изменений выборки (центр распределения) ![]() принимают за центр некоторого интервала, после чего легко находят границы и окончательное количество указанных интегралов так, чтобы в совокупности они перекрывали всю область от
принимают за центр некоторого интервала, после чего легко находят границы и окончательное количество указанных интегралов так, чтобы в совокупности они перекрывали всю область от ![]() до
до ![]() .
.
4) Возьмем часть вариационного ряда, для которого справедливо неравенство:
![]() . 1.3)
. 1.3)
Здесь ![]() – границы m-го интервала. Отметим, что при использовании формулы (1.3) значения
– границы m-го интервала. Отметим, что при использовании формулы (1.3) значения ![]() , попавшие на границу между (m – 1)-м и m-м интервалами, относят к m-му интервалу.
, попавшие на границу между (m – 1)-м и m-м интервалами, относят к m-му интервалу.
5) Подсчитывают относительное количество (относительную частоту) наблюдений Nm/N, попавших в данный квант.
6) Строят гистограмму, представляющую собой ступенчатую кривую, значение которой на m-м интервале ![]() (m=1,2,…,K) постоянно и равно Nm/N, или с учетом условия
(m=1,2,…,K) постоянно и равно Nm/N, или с учетом условия
![]()
равно:
![]() =
= ![]() .
.
Пример 2
Имеется выборка из 40 наблюдений, а соответствующий ей вариационный ряд имеет вид:
![]() .
.
По формуле (1.1) получаем:
![]() ;
;
 принимаем К = 7.
принимаем К = 7.
Тогда
![]() ;
;
выбираем ![]() .
.
Находим
![]()
![]() ,
,
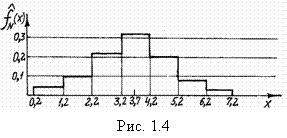
после чего строим гистограмму ![]() и легко определяем границы интервалов (рис. 1.4).
и легко определяем границы интервалов (рис. 1.4).
Допустим, после такой разбивки выяснилось, что в первый интервал попало два значения ![]() ; во второй – четыре: N2=4; в следующие: N3 = 9; N4 = 13; N5 = 8; N6 = 3; N7 = 1.
; во второй – четыре: N2=4; в следующие: N3 = 9; N4 = 13; N5 = 8; N6 = 3; N7 = 1.
2. Определение статистических оценок выборки. Математическое ожидание (среднее значение):
![]() (1.4)
(1.4)
есть наиболее вероятное значение числа в массиве выборки.
Смещенная дисперсия:
![]() (1.5)
(1.5)
является наиболее вероятной степенью отклонения xi от среднего значения ![]() .
.
Несмещенная дисперсия
![]() (1.6)
(1.6)
применяется при статической обработке чисел xi с нормальным распределением.
Среднеквадратичное стандартное (несмещенное) отклонение случайной величины равно:
![]() . (1.7)
. (1.7)
1. Проверка близости выборки к нормальному распределению случайной величины.
Коэффициент асимметрии
![]() (1.8)
(1.8)
характеризует скошенность графической функции плотности распределения вероятностей f(x). При А = 0 она симметрична, при A >0 вытянут правый, а при А < 0 – левый участок спада кривой f(x).
Коэффициент эксцесса
![]() (1.9)
(1.9)
характеризует степень остроты пика кривой f(x) в сравнении с f(x) для нормального распределения. Если E > 0, то f(x) имеет более острый пик, чем при нормальном распределении, если E < 0 – пик менее острый.
Вспомогательные коэффициенты вычисляют по формулам:
![]() , (1.10)
, (1.10)
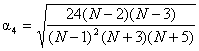 . (1.11)
. (1.11)
Они служат для приближенной проверки гипотезы о нормальном распределении xi. Если
![]() и
и ![]() ,
,
то распределение f(x) для массива xi можно считать нормальным.
Пример 3
Допустим, необходимо найти статистические оценки массива из 10 чисел xi:
9, 8, 10, 9, 11, 12, 10, 10, 9 и 11.
Используя формулы 1.4 — 1.11, получаем:
![]() ; D = 1,29;
; D = 1,29; ![]() ;
;
А = 0,1965658; Е = -0,753921; ![]() ;
;
![]() .
.