В любом нагретом (охлажденном) теле всегда есть точки, имеющие одинаковые температуры.  Соединив их,  получим  семейство изотермических поверхностей  (семейство  линий равных температур — изотерм).

На рис. 1.4 показано изменение температур станка на холостом ходу. Цифры у изотерм показывают фактическую температуру. В теплофизике для удобства расчетов оперируют избыточными температурами,  отсчитывае­мыми от некоторого условного нуля. Часто за начало отсчета при­нимают температуру окружающей среды   °С. Поэтому если бы мы хотели перейти к избыточным температурам, то на изо­термах следовало бы поставить значения от 0 до 8 °С. В дальнейшем, если специально не оговорено, следует понимать, что речь идет об избыточных температурах, и для определе­ния фактического значения температуры к результатам расчета надо добавлять 20 °С.

Градиент температуры – это вектор,  направленный по нормали  к  изотермической поверхности в  сторону возрастания температуры и численно равный изменению температуры на единице длины этой нормали.

Предел         ,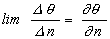

где n — расстояние, измеренное по нормали в данной точке к изотерме с меньшим значением температуры, представляет собой численное значение  градиента. Обозначая l_n единичный вектор, перпендикулярный к изотермической поверхности, запишем

.