Имеется еще один источник неопределенности, на котором в силу его важности и распространенности стоит остановиться отдельно. Речь идет о неопределенности в понимании цели операции. Часто имеется целый ряд показателей эффективности, желательность максимизации (или минимизации) которых не вызывает сомнения, но нет четких представлений о виде общего критерия, т.е. едином показателе. Такое положение дел является весьма характерным. Например, если проектируется новая модель самолета, то желательно, чтобы он имел минимальную массу, максимальную скорость и грузоподъемность, был высоконадежным и экономичным в эксплуатации, но так как эти требования противоречивы, то единый критерий эффективности предложить трудно.

Вопрос о введении единого (будем называть его общим) критерия эффективности в операции по ряду первичных (будем называть их частными) критериев находится в распоряжении оперирующей стороны. Варианты введения общего критерия называются методами свертки критериев эффективности.

Общий вид свертки следующий:

,

где  – общий критерий,  – частные критерии,  – некоторая (вообще говоря произвольная) функция.

Наиболее распространенными способами свертки критериев эффективности являются:

1) суммирование с весовыми коэффициентами;

2) переход от критериев количественных к качественным;

3) логические способы свертки;

4) обобщенные логические способы свертки.

Суммирование с весовыми коэффициентами. Этот способ наиболее распространен в экономических задачах, откуда происходит его второе название – экономический способ свертки:

.

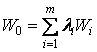Коэффициенты  называются весовыми и обычно удовлетворяют условию нормировки:

,

хотя это условие и не является обязательным. Остающаяся неточность знания цели может выражаться в неопределенности .

Переход от критериев количественных к качественным. Все критерии можно условно разбить на два типа: критерии, принимающие только два значения (чаще всего 0 и 1), и критерии, принимающие более двух (как правило, много) значений. Первые будем называть критериями качественного типа. Смысл их состоит в том, что все исходы операции они разбивают на две группы: удовлетворительные и неудовлетворительные. Вторые будем называть критериями количественного типа, при таких критериях цель операции состоит в получении возможно большего значения эффективности. От критериев качественного типа можно перейти к количественным следующим способом:

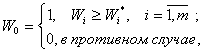
где через  обозначены пороговые (удовлетворительные) значения частных критериев. Исход операции удовлетворителен только в том случае, если по всем частным критериям достигнуты пороговые значения.

Логические способы свертки (для критериев качественного типа). Переменные, принимающие значения только 0 и 1, называются логическими (или булевыми). Операции с такими переменными носят название логических. Так как критерии качественного типа представляют собой булевы переменные, то для свертки качественных критериев можно использовать логические операции. Таких основных операций три:

1) отрицание (противоположная цель)

2) конъюнкция (логическое произведение, исход операции оценивается как удовлетворительный по общему критерию, если он удовлетворителен по всем частным критериям)

3) дизъюнкция (логическая сумма, для «успеха» по общему критерию достаточно «успеха» хотя бы по одному частному критерию), которую можно представить в виде:

.

Обобщенные логические способы свертки (для критериев количественного типа). Содержательными аналогами логических операций для количественных критериев служат следующие операции:

1) противоположная цель

2) оценка по наихудшему значению частных критериев (с учетом весовых коэффициентов)

3) оценка по наилучшему значению частных критериев

.

Зачастую оперирующая сторона затрудняется выбрать не только значения весовых коэффициентов, но и сам способ свертки критериев. В такой ситуации обычно вводят понятие оптимальности в терминах всего набора частных критериев (вектора критериев). Покажем это на примере наиболее известного понятия оптимальности по Парето.

Пусть имеется вектор критериев эффективности

,

зависящих для простоты только от стратегии  (неконтролируемых факторов нет). Здесь  – область возможных значений переменной .

Точка  называется эффективной точкой (или оптимальной по Парето стратегией), а вектор  – эффективным значением вектора критериев, если не существует такой точки

, что ,

причем хотя бы для одного  неравенство строгое

.