Будем предполагать, что рассматриваемые далее множества A, B, C, …, A_i, I,  над которыми выполняются операции, являются подмножествами некоторого множества U, которое называется универсумом. Далее через {x: P(x)} будем обозначать множество элементов xÎU, удовлетворяющих условию P(x).

Определим операции с помощью следующих формул, которые называются:

1) AÇB={x: xÎA & xÎB} – пересечением множеств A и B;

2) AÈB={x: xÎA Ú xÎB} –объединением;

3) AB={x: xÎA & ~(xÎB)} –теоретико-множественной разностью множеств;

4) ADB= AB È BA  – называется симметрической разностью;

5) =UA –дополнением множества A;

6)  A_i = {x: ($iÎI) xÎA_i} – объединением семейства множеств;

7) A_i = {x:("iÎI) xÎA_i} – пересечением семейства множеств.

Через  |A| будем обозначать количество элементов конечного множества.

Предложение

Пусть U – множество. Тогда для любых его подмножеств A, B и C верны равенства:

1) AÇB=BÇA, AÈB= BÈA, (коммутативность);

2) AÇ( BÇC) = (AÇ B)ÇC, AÈ(BÈC)=(AÈB)ÈC, (ассоциативность);

3) AÇ(AÈB) = AÈ(AÇB)= A (закон поглощения);

4) AÇ(BÈC) = (AÇB)È(AÇC);  AÈ (BÈC) = (AÈB)Ç(AÈC)  (дистрибутивность);

5) , ;

6) AÇA = A, AÈA = A;

7) AÈU = U, AÇÆ = Æ;

8) AÈÆ = A, AÇU = A;

9) ;

10) ,  (законы де Моргана).

Доказательство

Докажем, например, первое из свойств дистрибутивности (равенство 4). Для этой цели  нужно доказать, что левая часть равенства содержится в правой, и наоборот.

Пусть

xÎ AÇ(BÈC).

Тогда

x Î A   и         x Î BÈC.

И значит

(x Î A и x Î B)                      или                 (x Î A и x Î C).

Следовательно,

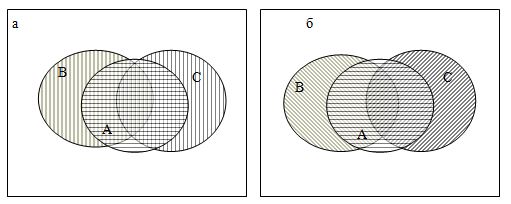
Рис. 1.1. Диаграммы Эйлера-Венна

x Î (AÇB)È(AÇC).

Эти свойства иллюстрируются с помощью  диаграмм Эйлера-Венна (рис. 1.1). Точки прямоугольников соответствуют элементам универсума U, точки кругов – подмножествам A, B, C. Элементы множеств B и C (см. рис. 1.1, а) заштрихованы вертикальными линиями. Отсюда, область, заштрихованная вертикальными линиями, будет соответствовать объединению BÈC. Элементы из A заштрихованы горизонтальными линиями. Следовательно,  область AÇ(BÈC) будет заштрихована в клетку.

Область B (см. рис. 1.1, б)  заштрихована косыми линиями, а область A – горизонтальными. Область AÇB будет заштрихована косыми и вертикальными линиями. Аналогично область AÇC будет заштрихована косыми и вертикальными линиями. Из рис.1.1 видно, что область (см. рис. 1.1, а), заштрихованная горизонтальными  и вертикальными линиями равна области (см. рис. 1.1, б), заштрихованной косыми  и горизонтальными линиями. Значит, соответствующие множества AÇ(BÈC) и  (AÇB)È(AÇC) равны.