Диаграммы Эйлера-Венна – геометрические представления множеств. Построение диаграммы заключается в изображении большого прямоугольника, представляющего универсальное множество U, а внутри его – кругов (или каких-нибудь других замкнутых фигур), представляющих множества. Фигуры должны пересекаться в наиболее общем случае, требуемом в задаче, и должны быть соответствующим образом обозначены. Точки, лежащие внутри различных областей диаграммы, могут рассматриваться как элементы соответствующих множеств. Имея построенную диаграмму, можно заштриховать определенные области для обозначения вновь образованных множеств.

Операции над множествами рассматриваются для получения новых множеств из уже существующих.

Определение. Объединением множеств А и В называется множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному из множеств А, В (рис. 1):

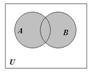
Рис. 1.1. Диаграмма Эйлера-Венна для объединения

Определение. Пересечением множеств А и В называется множество, состоящее из всех тех и только тех элементов, которые принадлежат одновременно как множеству А, так и множеству В (рис. 2):

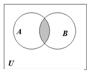
Рис. 1.2. Диаграмма Эйлера-Венна для пересечения

Определение. Разностью множеств А и В называется множество всех тех и только тех элементов А, которые не содержатся в В (рис. 3):

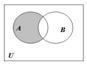
Рис. 1.3. Диаграмма Эйлера-Венна для разности

Определение. Симметрической разностью множеств А и В называется множество элементов этих множеств, которые принадлежат либо только множеству А, либо только множеству В (рис. 4):

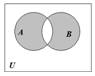
Рис. 1.4. Диаграмма Эйлера-Венна для симметрической разности

Определение. Абсолютным дополнением множества А называется множество всех тех элементов, которые не принадлежат множеству А (рис. 5):

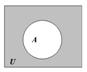
Рис. 1.5. Диаграмма Эйлера-Венна для абсолютного дополнения

Пример 5. С помощью диаграмм Эйлера – Венна проиллюстрируем справедливость соотношения  (рис. 6).

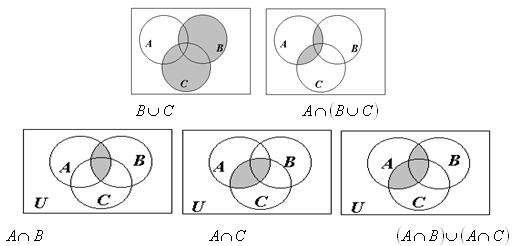
Рис. 1.6. Доказательство справедливости соотношения для примера 5

Убедились, что в обоих случаях получаем равные множества. Следовательно, исходное соотношение справедливо.