Простейшим примером финансовой сделки является однократное предоставление в долг некоторой суммы (PV) с условием, что через какое-то время (t) будет возвращена большая сумма (FV). При этом FV называется будущей стоимостью, а PV – настоящей стоимостью.
Будущая стоимость денег денег (FV) – это сумма инвестированных в настоящий момент денежных средств, в которую они превратятся через определенный период времени с учетом определенной ставки процента.
Настоящая стоимость денег (PV) – это сумма будущих денежных средств, приведенных с учетом определенной ставки процента (процентной ставки) к настоящему периоду времени.
Результативность приведенной сделки может быть охарактеризована:
· или с помощью абсолютного показателя (FV – PV), но как было уже сказано, абсолютные показатели не подходят для подобной оценки ввиду их несопоставимости во временном аспекте;
· или расчетом относительного показателя, специального коэффициента – ставки.
Ставка рассчитывается как отношение приращения исходной суммы к базовой величине, в качестве которой можно брать либо PV, либо FV. Таким образом, ставка рассчитывается по одной из двух формул:
· темп прироста
![]() ; (1.1)
; (1.1)
· темп снижения
![]() . (1.2)
. (1.2)
В финансовых вычислениях первый показатель имеет еще названия «процентная ставка», «процент», «ставка процента», «норма прибыли», «доходность», а второй – «учетная ставка», «дисконт».
Обе ставки взаимосвязаны, т.е. зная одну ставку, можно рассчитать другую:
![]() или
или ![]() .
.
Оба показателя могут выражаться либо в долях единицы, либо в процентах. Различие в формулах состоит в том, какая величина берется за базу сравнения:
· в формуле процентной ставки (1.1) за базу сравнения берется исходная сумма;
· в формуле учетной ставки (1.2) – возвращаемая сумма.
Очевидно, что ![]() , а степень расхождения зависит от уровня процентных ставок на конкретный момент времени. Например:
, а степень расхождения зависит от уровня процентных ставок на конкретный момент времени. Например:
· если it = 8 %, то dt = 7,4 %, т.е. расхождение сравнительно невелико;
· если it = 80 %, то dt = 44,4 %, т.е. ставки существенно различаются по величине.
Как мы видим, при разумных значениях ставок расхождения между процентной и дисконтной ставками относительно невелики и потому в прогнозных расчетах, например, при оценке инвестиционных проектов может быть использована любая из них.
Итак, в любой простейшей сделке всегда присутствуют три величины, две из которых заданы, а одна является искомой.
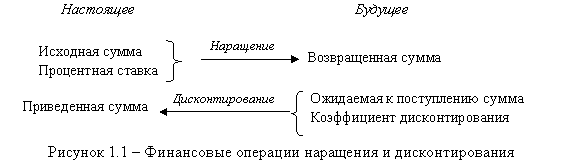
Процесс, в котором заданы исходная сумма и процентная ставка называется процессом наращения, а процесс, в котором заданы ожидаемая в будущем к получению (возвращаемая) сумма и коэффициент дисконтирования, называется процессом дисконтирования. В первом случае речь идет о движении денежного потока от настоящего к будущему, во втором – о движении денежного потока от будущего к настоящему (рисунок 1.1).
В качестве коэффициента дисконтирования может использоваться либо процентная ставка (математическое дисконтирование), либо учетная ставка (банковское дисконтирование).
Экономический смысл операции наращения (формула 1.1.) состоит в определении величины той суммы, которой будет или желает располагать инвестор по окончании этой операции. Поскольку из формулы (1.1) получается:
![]()
и
![]() ,
,
то видно, что время генерирует деньги. Величина FV показывает будущую стоимость «сегодняшней» величины PV при заданном уровне доходности.
На практике доходность является величиной непостоянной, зависящей, главным образом, от степени риска, ассоциированного с данным видом бизнеса. Связь здесь прямо пропорциональная: чем рискованнее бизнес, тем выше значение доходности.
Экономический смысл дисконтирования заключается во временном упорядочении денежных потоков различных временных периодов. Коэффициент дисконтирования показывает, какой ежегодный процент возврата хочет (или может) иметь инвестор на инвестируемый им капитал. В этом случае искомая величина PV показывает как бы текущую, сегодняшнюю стоимость будущей величины FV. Например, предприятие получило кредит на один год в размере 5 млн. руб. с условием возврата 10 млн. руб. в этом случае процентная ставка равна 100 %, а дисконт – 50 %.