Из курса теоретических основ электротехники известно, что любой замкнутый круговой ток создает магнитный момент:
,
где 
– сила тока, А; 
– площадь, обтекаемая током, 
.
Аналогично вращающийся по орбите электрон создает так называемый орбитальный магнитный момент 
.
Вследствие вращения электрона вокруг своей оси возникает спиновый магнитный момент 
. Так же, как и ток, орбитальный и спиновый моменты – величины векторные. Направление их определяется по правилу буравчика, как показано на рис. 1.1, а.
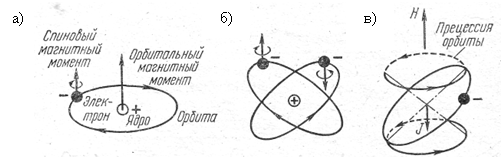
Рис. 1.1. Магнитные моменты электрона в атоме
Если атом имеет несколько электронов, полный или собственный магнитный момент атома определяется векторной суммой всех орбитальных и спиновых моментов с учетом их направления. Поэтому в любой полностью заполненной оболочке, как, например, у атома гелия (рис. 1.1, б), спиновые и орбитальные моменты взаимно компенсируются, т.к. электроны на орбитах располагаются парами и имеют противоположные направления вращения, и собственный магнитный момент такого атома при отсутствии внешнего поля равен нулю.
Суммарный магнитный момент единицы объема вещества называют намагниченностью, Aм2/м3 или А/м:
где 
– сумма всех магнитных моментов атома, занимающих объем V.
Если на атом действует внешнее магнитное поле Н, то возникает прецессия орбит электронов вокруг вектора этого поля (на рис. 1.1, в показана пунктиром), что эквивалентно дополнительному вращению электронов. При этом возникает дополнительный, наведенный магнитный момент. По правилу Ленца он всегда направлен против внешнего поля Н и стремится ослабить его. Это явление называют диамагнетизмом. Оно
присуще атомам всех веществ. Но для некоторых веществ диамагнитный момент равен нулю.
Любопытно отметить, что намагниченность 
имеет ту же размерность, что и напряженность А/м. Следовательно, намагниченность можно рассматривать как напряженность, созданную микротоками электронных оболочек атомов. Поэтому индукцию в веществе при наличии внешнего поля напряженностью Н можно представить как:
.
Если векторы 
и имеют одинаковое направление, можно перейти к скалярному выражению и разделить обе части выражения на Н:
.
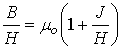Отношение 
называют магнитной восприимчивостью вещества. Следовательно:
.