В разд. 1.2 получили определение поверхностного интеграла первого рода по площади поверхности формула (1.37). Ставим задачу для его вычисления.
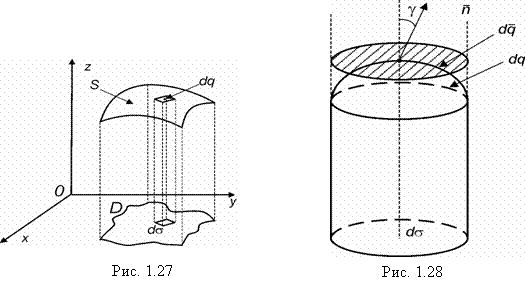
Пусть задана поверхность S (рис. 1.27) и на ней функция f(x, y, z).
Функцию f(x, y, z) нельзя смешивать с функцией, входящей в уравнение поверхности S. Будем считать, что поверхность S задана явно: ![]() .
.
Известна связь: площадь проекции плоской фигуры равна площади самой фигуры, умноженной на абсолютную величину косинуса двугранного угла между плоскостями, т.е.
![]() . (1.76)
. (1.76)
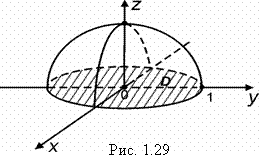
Проведем в точке ![]() , касательную плоскость (рис. 1.28) – фрагмент разбиения:
, касательную плоскость (рис. 1.28) – фрагмент разбиения:
![]() (1.77)
(1.77)
где X, Y, Z – координаты текущей точки плоскости.
Заменим изогнутый элемент dq плоским ![]() , лежащим в плоскости (на рис 1.28 заштрихован), имеющим ту же проекцию
, лежащим в плоскости (на рис 1.28 заштрихован), имеющим ту же проекцию ![]() , что и dq. Можно приближенно считать:
, что и dq. Можно приближенно считать: ![]() .
.
 Нормальный вектор
Нормальный вектор ![]() согласно формуле (1.77) имеет координаты:
согласно формуле (1.77) имеет координаты: ![]() . Поэтому для угла
. Поэтому для угла ![]() между плоскостями касательной и xОy получим соотношение:
между плоскостями касательной и xОy получим соотношение:
![]() ,
,
тогда, учитывая формулу (1.76), имеем: ![]() . Или
. Или
![]() . (1.78)
. (1.78)
Так как на поверхности S: z = z(x, y), то ![]() . Учтя это, получим:
. Учтя это, получим:
![]() (1.79)
(1.79)
 Формула (1.79) говорит о том, что поверхностный интеграл первого рода сводится к двойному интегралу.
Формула (1.79) говорит о том, что поверхностный интеграл первого рода сводится к двойному интегралу.
Пример
Найти площадь части параболоида ![]() , расположенной над плоскостью xОy (рис. 1.29).
, расположенной над плоскостью xОy (рис. 1.29).
Решение. Поверхность задана явно, поэтому находим:
![]()
![]()
![]()
По свойству (1.44) с применением полярных координат получим:
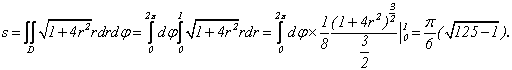
Замечание. Можно получить и другие формулы для вычисления поверхностного интеграла первого рода, проектируя поверхность S на плоскости xОz и yОz (рекомендуется записать их самостоятельно).