Частотой отказов называется отношение числа отказавших образцов аппаратуры в единицу времени к числу образцов, первоначально установленных на испытание при условии, что отказавшие образцы не восстанавливаются и не заменяются исправными.

Так как число отказавших образцов в интервале времени может зависеть от расположения этого промежутка по оси времени, то частота отказов является функцией времени. Эта характеристика в дальнейшем обозначается α(t).

Согласно определению

,                                                    (1.10)

где n(t) – число отказавших образцов в интервале времени от  до ; N_{0 –} число образцов аппаратуры, первоначально установленных на испытание;  – интервал времени.

Выражение (1.10) является статистическим определением частоты отказов. Этой количественной характеристике надежности легко дать вероятностное определение. Вычислим в выражении (1.10) n (t), т.е. число образцов, отказавших в интервале. Очевидно,

n(t) = -[N(t + ) – N(t)],                                            (1.11)

где N(t) – число образцов, исправно работающих к моменту времени t; N(t + ) – число образцов, исправно работающих к моменту времени t + .

При достаточно большом числе образцов (N₀) справедливы соотношения:

N(t) = N₀P(t);

N(t+) = N₀P(t+).                                             (1.12)

Подставляя выражение (1.11) в выражение (1.10) и учитывая выражение (1.12), получим:

,

а с учетом выражения (1.4) получим:

α(t) = Q^/(t)                                                       (1.13)

Из выражения (1.13) видно, что частота отказов характеризует плотность распределения времени работы аппаратуры до ее отказа. Численно она равна взятой с обратным знаком производной от вероятности безотказной работы. Выражение (1.13) является вероятностным определением частоты отказов.

Таким образом, между частотой отказов, вероятностью безотказной работы и вероятностью отказов при любом законе распределения времени возникновения отказов существуют однозначные зависимости. Эти зависимости на основании (1.13) и (1.4) имеют вид:

;                                                        (1.14)

.                                                      (1.15)

Частота отказов, являясь плотностью распределения, наиболее полно характеризует такое случайное явление, как время возникновения отказов. Вероятность безотказной работы, математическое ожидание, дисперсия и т.п. являются лишь удобными характеристиками распределения и всегда могут быть получены, если известна частота отказов α(t). В этом ее основное достоинство как характеристики надёжности.

Характеристика α(t) имеет также существенные недостатки. Эти недостатки становятся ясными при детальном рассмотрении выражения (1.10). При определении a(t) из экспериментальных данных фиксируется число отказавших образцов n(t) за промежуток времени  при условии, что все отказавшие ранее образцы не восполняются исправными. Это означает, что частоту отказов можно использовать для оценки надежности только такой аппаратуры, которая после возникновения отказа не ремонтируется и в дальнейшем не эксплуатируется (например, аппаратуры разового использования, простейших элементов, не поддающихся ремонту, и т.п.). В противном случае частота отказов характеризует надежность аппаратуры лишь до первого ее отказа.

Оценить с помощью частоты отказов надежность аппаратуры длительного пользования, которая может ремонтироваться, затруднительно. Для этой цели необходимо иметь семейство кривых α(t), полученных: до первого отказа, между первым и вторым, вторым и третьим отказами и т.д. Следует, однако, заметить, что при отсутствии старения аппаратуры указанные частоты отказов будут совпадать. Поэтому α(t) хорошо характеризует надежность аппаратуры также в том случае, когда отказы подчиняются экспоненциальному распределению.

Надежность аппаратуры длительного использования можно характеризовать частотой отказов, полученной при условии замены отказавшей аппаратуры исправной. При этом внешне формула (1.10) не изменяется, однако меняется ее внутреннее содержание.

Частота отказов, полученная при условии замены отказавшей аппаратуры исправной (новой или восстановленной), иногда называется средней частотой отказов и обозначается .

Средней частотой отказов называется отношение числа отказавших образцов в единицу времени к числу испытываемых образцов при условии, что все образцы, вышедшие из строя, заменяются исправными (новыми или восстановленными).

Таким образом,

,                                                     (1.16)

где n(t) – число отказавших образцов в интервале времени от  до , N₀ – число испытываемых образцов (N₀ остается в процессе испытания постоянным, так как все отказавшие образцы заменяются исправными),  – интервал времени.

Средняя частота отказов обладает следующими важными свойствами:

1) . Это свойство становится очевидным, если учесть, что ;

2) независимо от вида функции α(t) при  средняя частота отказов стремится к некоторой постоянной величине;

3) главное достоинство средней частоты отказов как количественной характеристики надежности состоит в том, что она позволяет довольно полно оценить свойства аппаратуры, работающей в режиме смены элементов. К такой аппаратуре относятся сложные автоматические системы, предназначенные для длительного использования. Подобные системы после возникновения отказов ремонтируются и затем вновь эксплуатируются;

4) средняя частота отказов может быть также использована для оценки надежности сложных систем разового применения в процессе их хранения;

5) она также довольно просто позволяет определить число отказавших в аппаратуре элементов данного типа. Это свойство  может быть использовано для вычисления необходимого количества элементов для нормальной эксплуатации аппаратуры в течение времени t. Поэтому является наиболее удобной характеристикой для ремонтных предприятий;

1) знание  позволяет также правильно спланировать частоту профилактических мероприятий, структуру ремонтных органов, необходимое количество и номенклатуру запасных элементов.

К недостаткам средней частоты отказов следует отнести сложность определения других характеристик надежности, и в частности основной из них вероятности безотказной работы, при известной .

Сложная система состоит из большого числа элементов. Поэтому представляет интерес найти зависимость средней частоты отказов. Введем понятие суммарной частоты отказов сложной системы.

Суммарной частотой отказов называется число отказов аппаратуры в единицу времени, приходящееся на один ее экземпляр.

В дальнейшем эта характеристика обозначается . Согласно определению, для одного образца

,                                                       (1.17)

где n (t) – число отказов аппаратуры за время от  до ;   – интервал времени.

Если для определения  используется несколько образцов, то суммарная частота отказов вычисляется по формуле:

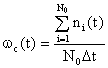,                                                   (1.18)

где n_i(t) – число отказов i-го образца аппаратуры за время от  до ; N_{0 –} число испытываемых образцов аппаратуры;  — интервал времени,.

Отказы сложной системы состоят из отказов отдельных элементов, поэтому число отказов n(t) аппаратуры в выражении (1.18) будет равно сумме всех отказов элементов. Если N_i-число элементов i-го типа, а  — средняя частота отказов элементов i-го типа, то за промежуток времени произойдет отказов элементов i-го типа, а всего отказов будет:

где r – число типов элементов.

Подставляя выражение для n (t) в формулу (1.18), получим:

                                                 (1.19)

т.е. суммарная частота отказов сложной системы в момент времени t равна сумме средних частот отказов элементов.