Пусть получена выборка из двумерной совокупности при наблюдении двух случайных величин X и Y (табл. 1.1).

Обработку результатов наблюдений в данном случае можно осуществлять по следующей схеме:

1.

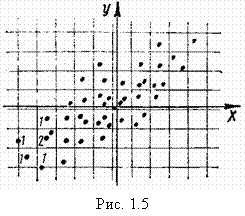Построение поля рассеяния, как правило, это первый шаг при обработке результатов наблюдений двумерной совокупности случайных величин X, Y. Для этого на плоскости с координатами x, y отмечают экспериментальные точки. Возможный вид такого поля изображен на рис. 1.5.

2. Составление таблицы двумерного распределения. Эту таблицу составляют следующим образом. Оси O_x и O_y разбивают на отдельные интервалы длиной и . Значения , , количество К_х, К_y и размещение этих интервалов для каждой из переменных X и Y находят с помощью правил, изложенных в подразделе 1.2. Соответствующие границы наносят на диаграмму рассеяния (рис. 1.5) и затем подсчитывают количество точек (), попавших в каждый из образовавшихся прямоугольников (при условии, что если какая-либо точка расположена на границе, то ее относят к правому или верхнему прямоугольнику). Далее составляют таблицу (табл. 1.2).

В таблицу 1.2 заносят величины , а также относительные величины . Подобную таблицу можно использовать как исходную для построения гистограмм и диаграмм накопленных частот в трехмерном пространстве, которые являются эмпирическими аналогами двумерного интегрального закона и двумерной функции распределения.

Таблица 1.2

Отметим, что с помощью таблицы двумерного распределения (табл. 1.2) легко получить исходные данные для построения гистограмм, соответствующих каждой из двух одномерных случайных величин X и Y. Для этого достаточно просуммировать значения таблицы либо по каждому столбцу (при построении гистограммы для Y), либо по каждой строке (при построении гистограммы для Х).

1. Вычисление оценки коэффициента корреляции производят по формуле:

,                                 (1.23)

где ,  и s_x, s_y находят с помощью формул (1.4) – (1.6).

Отметим, что между значением и знаком коэффициента корреляции, с одной стороны, и видом рассеяния – с другой, существует определенная связь. Если начало координат перенести в точку (; ), то:

1) при p > 0 точки на диаграмме рассеяния группируются в основном в I и III квадрантах, а при p < 0 – в квадрантах II и IV;

2) при  точки беспорядочно разбросаны во всех четырех квадрантах; при  точки группируются на прямых (находящихся либо в квадрантах I и III, либо в квадрантах II и IV).