Для произвольных множеств А, В, и С справедливы следующие соотношения (табл. 1):
Таблица 1.1 Основные тождества алгебры множеств
|
1. Коммутативность объединения
|
1′. Коммутативность пересечения
|
|
2. Ассоциативность объединения
|
2′. Ассоциативность пересечения
|
|
3. Дистрибутивность объединения относительно пересечения
|
3′. Дистрибутивность пересечения относительно объединения
|
|
4. Законы действия с пустым и универсальным множествами
|
4′. Законы действия с пустым и универсальным множествами
|
|
5. Закон идемпотентности объединения
|
5′. Закон идемпотентности пересечения
|
|
6. Закон де Моргана
|
6′. Закон де Моргана
|
|
7. Закон поглощения
|
7′. Закон поглощения
|
|
8. Закон склеивания
|
8′. Закон склеивания
|
|
9. Закон Порецкого
|
9′. Закон Порецкого
|
|
10. Закон двойного дополнения
|
|
Пример 6.
Доказать следующее тождество ![]() .
.
Решение.
Докажем это тождество двумя способами: аналитически (используя равносильности алгебры множеств) и конструктивно (используя диаграммы Эйлера-Венна).
1) ![]()
2) Построим соответствующие диаграммы Эйлера-Венна (рис. 7).
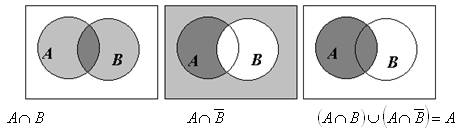
Рис. 1.7. Доказательство справедливости тождества из примера 6