Полем называется область пространства, каждой точке Р которой поставлена в однозначное соответствие некоторая величина Q(p).

Если величина  Q(p)  является физической, то поле называется физическим. В зависимости от природы функции Q(p), поля разделяются на скалярные  и  векторные. Примерами скалярных физических полей могут быть поля температуры, атмосферного давления, плотности воздуха, электрического потенциала, массы и т.д. К векторным величинам относятся: поля силы тяжести, скорости частиц текущей жидкости (газа), сдвига точек упругого тела, магнитной индукции и др.

Если функция Q(p) не изменяется с течением времени, то поле называется стационарным или установившимся, в противном случае – нестационарным.

Для получения общих результатов, справедливых для любых конкретных физических полей, всякому полю ставится в соответствие его математическая модель. Математическая теория поля изучает свойства векторных и скалярных полей, которые выявляются практическими задачами из физики, электротехники, математики и других наук.

Для успешного овладения теорией поля необходим математический аппарат, в который входит векторная алгебра и векторный анализ, элементы дифференциального и интегрального исчисления. Отметим, что в перспективе обобщением теории скалярных и векторных полей является теория тензорных полей, которая играют важную роль в теории упругости, теории относительности и др.

Для задания скалярного поля надо задать скалярную функцию . Введем понятие поверхности (линии) равного уровня скалярного поля.

Определение. Поверхностью равного уровня скалярного поля  называется такая поверхность, на которой функция имеет постоянное значение.

Уравнение поверхности уровня:

,                                                             (1.90)

где       С – постоянная. Если функция , то говорят о линии равного уровня: .

При различных значениях С получаем семейство поверхностей (линий) уровня. Примерами поверхностей уровня являются поверхности: равных температур в некотором теле; равного потенциала V в электрическом поле .

Совокупность поверхностей (линий) уровня дает наглядное представление конкретного поля, что облегчает его изучение.

Пример 1

Найти поверхность уровня поля , проходящую через точку .

Решение. Уравнение поверхности уровня: U = C:

Очевидно, . Поверхностями уровня служит семейство сфер с центром в начале координат. Чтобы выбрать нужную сферу, проходящую через , требуется подставить координаты этой точки в уравнение поверхностей уровня:

Уравнение искомой поверхности уровня:

описывает сферу радиуса R = 3 с центром в начале координат.

Пример 2

Найти линии уровня поля .

Решение. Положим ; .

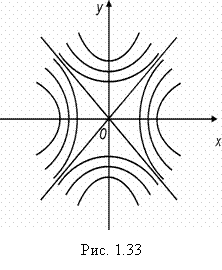
При С > 0 линии уровня есть равнобочные гиперболы с вершинами на оси Ох; при С = 0 – прямые  – асимптоты этих гипербол (сопряженных) (рис. 1.33).

Понятие скалярного поля тесно связано с важным понятием производной скалярной функции  по заданному направлению (в математическом анализе этого не было).

Теорема: если функция  дифференцируема в точке Р, то производная  в точке Р по любому направлению  существует и равна (обозначается ):

                                     (1.91)

Доказательство. Как известно из математического анализа [6], если функция дифференцируема, то её приращение (рис. 1.34) равно:

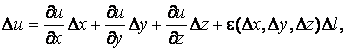
где       , когда .

Разделим на  обе части последнего равенства, получим:

Переходя к пределу при , и учитывая, что

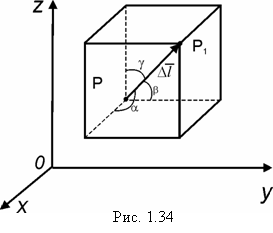
получим формулу (1.91). Если , то поле возрастает; при  – убывает и  – дает скорость изменения поля в направлении .

Пример 3

Найти производную от функции  по направлению  от точки Р(1; 1; 1) к точке Р₁(2; 3; 4).

Решение. Найдем:

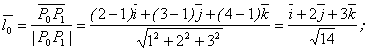
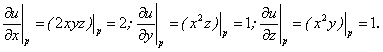
Следовательно,

Формула (1.91) ставит задачу: найти то направление, которое доставляет максимальное значение для . Оказывается, такое направление дается понятием градиента скалярного поля.

Определение. Градиентом скалярного поля (обозначается grad U) называется вектор, проекции которого на оси декартовой системы координат есть , , , т.е.

                                           (1.92)

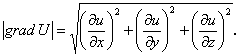                                           1.93)

Вывод: градиент скалярного поля есть вектор.

Имеется связь между производной по направлению и градиентом (рис. 1.35).

Найдем скалярное произведение :

.

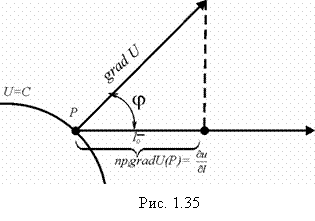
Таким образом, левая часть полученного равенства есть .

Итак,

           (1.94)

При изменении  будет меняться и . Очевидно, эта проекция будет максимальной, когда направление  совпадает с . Учитывая физический смысл производной по направлению и формулу (1.94) убеждаемся в том, что: вектор grad U по величине  и направлению есть наибольшая скорость возрастания . В этом состоит физический смысл градиента. Это широко используется в практике.

Покажем, что  направлен по нормали к поверхности (линии) уровня скалярного поля , проходящей через точку Р.

Уравнение поверхности уровня: . Уравнение нормали к поверхности уровня:

,

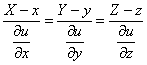где       X, Y, Z –  текущие координаты нормали; x, y, z – координаты поверхности, в которой проведена нормаль. Видим, что проекции направляющего вектора  нормали те же, что и градиента.

Пример 4

Найти наибольшую скорость возрастания скалярного поля  в точке Р(1; 2; 3).

Решение. Согласно (1.92) имеем:

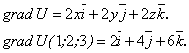
Согласно (1.93):

Значит,                                      

Поверхность уровня поля U, проходящая через точку Р(1; 2; 3) – сфера: . Наибольшая скорость возрастания функции U будет в направлении радиуса этой сферы, проходящего через данную точку Р(1; 2; 3).