Основные определения
Рассмотрим вероятностное пространство (
).
Однозначная числовая функция, заданная на пространстве элементарных исходов, называется случайной величиной (обозначения: 
, …).
Значения функции 
будем называть возможными значениями случайной величины 
. Таким образом, 
, 
.
В соответствии с определением, случайная величина каждому элементарному исходу из пространства 
, в зависимости от случая, ставит в соответствие одно определенное числовое значение.
Приведем несколько примеров случайных величин.
Пример 1
Эксперимент – подбрасывание игральной кости.
Пространство элементарных исходов:
,
где 
– на грани игральной кости выпало 
очков, 
.
Пусть 
– число очков, выпавших на грани игральной кости.
Возможные значения : 1, 2, …, 6.
Пример 2
Эксперимент – регистрация вызовов в течение часа на автоматической телефонной станции (АТС).
Пространство элементарных исходов:
.
Пусть 
– число вызовов, поступивших на АТС в течение часа.
Возможные значения : 0, 1, …
Если пространство элементарных исходов, на котором задается случайная величина, конечное (пример 1) или счётное (пример 2), то эта случайная величина называется дискретной (принимает отдельные изолированные значения).
Если пространство элементарных исходов бесконечное, несчётное и связное, то случайная величина называется непрерывной (имеет несчетное множество значений).
Закон распределения дискретной случайной величины
Пусть пространство элементарных исходов 
– конечное или счётное множество. Во втором случае будем считать, что n равно бесконечности.
Наибольший интерес представляют вероятности, с которыми случайная величина принимает каждое из своих возможных значений.
Обозначим через 
событие, которое заключается в том, что m принимает своё i-е значение, 
. Появление события 
означает, что в результате эксперимента имел место элементарный исход 
, поэтому
.
Множество пар чисел 
называется законом распределения дискретной случайной величины.
Закон распределения обычно представляется в виде таблицы, состоящей из двух строк, в первой из которых записываются возможные значения случайной величины, а во второй – вероятности, с которыми эти возможные значения принимаются:
|
|
|
|
… |
|
|
|
|
|
… |
|
При этом 
, так как по определению 
и
,
где – несовместные события.
Основные дискретные распределения
Равномерное распределение на множестве чисел: 
Возможные значения исходов и вероятностей:
.
|
|
|
|
… |
|
|
|
|
|
… |
|
.
Биномиальное распределение
В последовательности из n независимых испытаний схемы Бернулли, 
– число появлений события А в этих испытаниях.
Возможные значения исходов и вероятностей:
: 
;
.
|
|
|
|
… |
|
… |
|
|
|
|
|
… |
|
… |
|
.
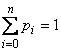Распределение Пуассона
Рассмотрим последовательность независимых испытаний при 
, случайная величина – число появлений события 
в этих испытаниях.
Возможные значения исходов и вероятностей:
m: 0, 1, 2, …;
.
|
|
|
… |
|
… |
|
|
|
… |
|
… |
.
Геометрическое распределение
Рассмотрим последовательность независимых испытаний. Случайная величина 
– число испытаний, проведённых до первого появления события А.
Возможные значения исходов и вероятностей:
m: 1, 2, 3, …;
.
|
|
1 |
2 |
… |
|
… |
|
|
|
|
… |
|
… |
.
Гипергеометрическое распределение
Имеется 
объектов произвольной природы. Среди них 
объектов обладают некоторым свойством 
. Наудачу отбираются 
объектов. Случайная величина – число объектов среди отобранных, обладающих свойством 
.
Возможные значения m: 
,
где
; 
.
При этом
.
Функция распределения случайной величины
Функция 
, равная вероятности того, что случайная величина примет значение меньшее 
, называется функцией распределения этой случайной величины , т. е.
. (1.20)
Геометрически, функция распределения – это вероятность того, что случайная величина примет значение, которое расположено на числовой оси левее точки .
Пусть дискретная случайная величина, заданная законом распределения:
|
|
|
|
… |
|
|
|
|
|
… |
|
.
Построим функцию распределения этой случайной величины.
Для удобства предположим, что 
, тогда
1) если 
, то
;
2) если 
, то
.
3) если 
, то
;
4) если рассматривается k-й промежуток 
, то
;
5) если 
, то
.
График функции распределения дискретной случайной величины (1.20) имеет вид (рис. 1.11).
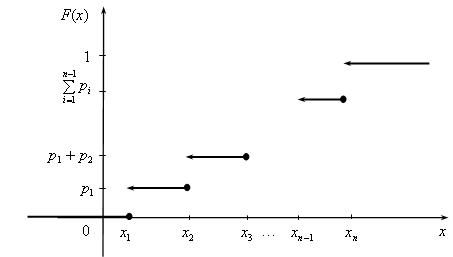
Рис. 1.11. График функции распределения дискретной случайной величины
Для любой дискретной случайной величины функция распределения есть кусочно-постоянная функция.
Случайная величина 
называется непрерывной, если её функция распределения непрерывна.
Основные свойства функции распределения:
1) функция распределения ограничена 
, так как функция распределения – это вероятность появления некоторого случайного события;
2) 
– неубывающая функция, т.е.
.
Следствие 1. Из последнего равенства следует, что
.
Следствие 2. Вероятность того, что непрерывная случайная величина примет одно из своих возможных значений равна нулю, т.е.
!
1) 
.
Плотность распределения вероятностей непрерывной случайной величины
Плотностью распределения вероятностей непрерывной случайной величины 
называется первая производная от функции распределения, т.е.
.
Здесь F(x) есть первообразная функции f(x):
.
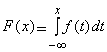Плотность распределения вероятностей обладает следующими свойствами:
1) неотрицательностью:
.
2) нормированностью:
.
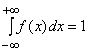В частности, если все возможные значения случайной величины принадлежат отрезку 
, то
.
Распределение непрерывных случайных величин может быть:
· равномерное;
· показательное (экспоненциальное);
· нормальное.
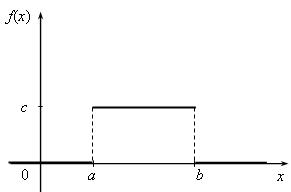
Рис. 1.12. Функция плотности вероятности равномерно распределенной случайной величины
Случайная величина равномерно распределена на [a, b], если функция плотности вероятностей имеет вид (рис. 1.12):
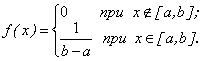
Функция распределения:
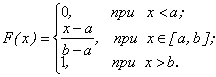
Случайная величина имеет показательное (экспоненциальное) распределение с параметром 
, если
, 
.
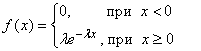Функция распределения имеет вид (рис. 1.13):
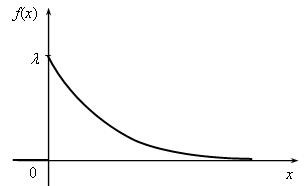
Рис. 1.13. Функция показательного (экспоненциального) распределения
Случайная величина имеет нормальное распределение с параметрами 
, если
, 
.
Функция распределения выражается через интегральную функцию Лапласа (рис. 1.14):
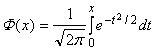
и равна
.
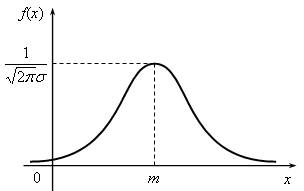
Рис. 1.14. Функция нормального распределения