Математическим ожиданием случайной величины  называется число, равное сумме попарных произведений возможных значений случайной величины на вероятности, с которыми эти значения принимаются. Математическое ожидание обозначается: .

Таким образом, по определению математическое ожидание равно:

.

Математическое ожидание  приближенно равно (и тем точнее, чем больше число испытаний) среднему значению, принимаемому случайной величиной.

Математическое ожидание имеет следующие свойства:

1) , с – const;

2)  (используемая функция );

3)  (используемая функция  );

4) если  – независимые случайные величины, то

.

Величина, характеризующая разброс возможных значений случайной величины относительно среднего значения, называется дисперсией. Обозначается: .

По определению дисперсия равна математическому ожиданию квадрата отклонения случайной величины от её математического ожидания :

.

Также может быть использована формула:

или

.

Дисперсии обладает следующими следующие свойствами:

1) ;

2) ;

3) если  – независимые случайные величины, то

;

;

4) .

Средним квадратическим отклонением  случайной величины  называется корень квадратный из дисперсии, т.е. по определению

.

Основные законы распределения дискретных случайных величин имеют следующие числовые характеристики:

1) равномерное распределение:

;           ;         .

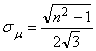2) биноминальное распределение:

.

, , .

3) распределение Пуассона:

,         ;

;      .

4) геометрическое распределение:

;      ;    ;              .