Математическим ожиданием непрерывной случайной величины 
с плотностью распределения вероятностей 
называется число 
, равное
.
Как и для дискретных случайных величин, здесь 
– среднее значение случайной величины.
Математическое ожидание непрерывной случайной величины обладает следующими свойствами:
1) 
, с – const;
2) 
(используемая функция 
);
3) 
(используемая функция 
).
4) если 
– независимые случайные величины, то
.
Дисперсия равна математическому ожиданию квадрата отклонения случайной величины от её математического ожидания 
,
,
.
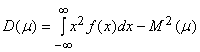Основные законы распределения непрерывных случайных величин имеют следующие числовые характеристики:
1) равномерное распределение:
· функция распределения:
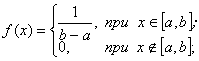
· математическое ожидание:
;
· дисперсия:
;
· среднее квадратическое отклонение:
.
2) показательное (экспоненциальное) распределение:
· функция распределения:
.
· математическое ожидание:
;
· дисперсия:
;
· среднее квадратическое отклонение:
.
3) нормальное распределение:
· функция распределения:
;
· математическое ожидание:
;
· дисперсия:
;
· среднее квадратическое отклонение:
.