Возьмем поле ![]() и некоторую кривую AB (рис. 1.41). Пусть
и некоторую кривую AB (рис. 1.41). Пусть ![]() — радиус-вектор точки M на кривой.
— радиус-вектор точки M на кривой.
Определение 1: криволинейный интеграл![]() , взятый по некоторой направленной линии AB , называется линейным инте
, взятый по некоторой направленной линии AB , называется линейным инте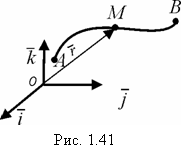 гралом от вектора
гралом от вектора ![]() вдоль линии AB.
вдоль линии AB.
Определение 2: Циркуляцией векторного поля ![]() вдоль замкнутой кривой K, называется линейный интеграл по этой замкнутой кривой K, обозначаемый через Г и определяемый формулой:
вдоль замкнутой кривой K, называется линейный интеграл по этой замкнутой кривой K, обозначаемый через Г и определяемый формулой:
![]() . (1.106)
. (1.106)
Если ![]() – силовое поле, то линейный интеграл от вектора
– силовое поле, то линейный интеграл от вектора ![]() равен работе сил поля при перемещении точки по кривой AB. В этом состоит физический смысл линейного интеграла (ранее мы называли криволинейным интегралом по координатам).
равен работе сил поля при перемещении точки по кривой AB. В этом состоит физический смысл линейного интеграла (ранее мы называли криволинейным интегралом по координатам).
Определим еще одну важную характеристику теории поля, которую называют вихрем (ротором) векторного поля.
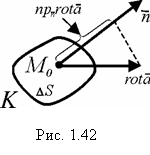 Возьмем в поле вектора
Возьмем в поле вектора ![]() точку
точку ![]() (рис. 1.42). Пусть
(рис. 1.42). Пусть ![]() - достаточно малая поверхность, содержащая точку
- достаточно малая поверхность, содержащая точку ![]() , К – контур этой поверхности,
, К – контур этой поверхности, ![]() - нормаль к
- нормаль к ![]() . Обход согласован с
. Обход согласован с ![]() и является положительным, Вычислим циркуляцию
и является положительным, Вычислим циркуляцию ![]() .
.
Предположим, что существует
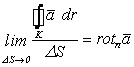 , (1.107)
, (1.107)
где ![]() . Такой вектор обозначается
. Такой вектор обозначается ![]() и называется вихрем (ротором) векторного поля
и называется вихрем (ротором) векторного поля ![]() .
.
Говорят, что векторное поле ![]() порождает другое векторное поле – поле
порождает другое векторное поле – поле ![]() и является векторной характеристикой векторного поля. Вектор
и является векторной характеристикой векторного поля. Вектор ![]() в данной точке поля
в данной точке поля ![]() обладает свойством: если нормаль
обладает свойством: если нормаль ![]() к
к ![]() совподает с направлением
совподает с направлением ![]() , то циркуляция
, то циркуляция ![]() имеет наибольшее значение, по сравнению с циркуляцией, при любом другом положении площадки
имеет наибольшее значение, по сравнению с циркуляцией, при любом другом положении площадки ![]() .
.
Понятие вихря введено независимо от выбора системы координат, т.е. служит инвариантной формулой (1.107).
Для удобства запоминания вихрь вектора ![]() записывают в декартовой системе в виде символического определения:
записывают в декартовой системе в виде символического определения:
 . (1.108)
. (1.108)
Раскрывая определитель по первой строке, будем иметь:
 . (1.109)
. (1.109)
Из (1.109) видно, что ![]() есть вектор. Если рассматривать векторное поле как поле скоростей частиц текущей жидкости, то ротор характеризует угловую скорость вращения малого объёма, окружающего точку. Поэтому
есть вектор. Если рассматривать векторное поле как поле скоростей частиц текущей жидкости, то ротор характеризует угловую скорость вращения малого объёма, окружающего точку. Поэтому ![]() характеризует вращательную способность поля
характеризует вращательную способность поля ![]() .
.
Пример 1
Найти ![]() , если
, если ![]() .
.
Решение. В нашем случае ![]() тогда
тогда
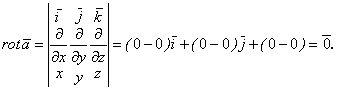
Пример 2
Найти ![]() , если
, если ![]() .
.
Решение
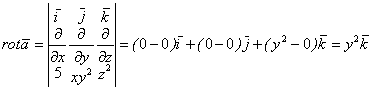 .
.
Пример 3
Найти ![]() , где
, где ![]() – линейные скорости точек вращающегося тела вокруг неподвижной точки с постоянной угловой скоростью
– линейные скорости точек вращающегося тела вокруг неподвижной точки с постоянной угловой скоростью ![]() ;
; ![]() .
.
Решение. Вектор ![]() в координатной форме учитывая, что
в координатной форме учитывая, что ![]() запишем так:
запишем так:
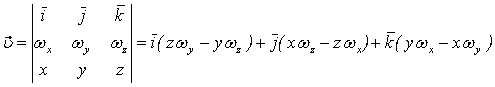 .
.
Согласно (1.109):
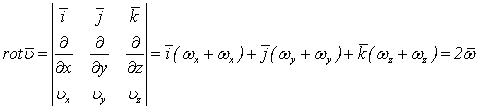 .
.