Поскольку форма импульсов на выходе ИЭ может быть самой разнообразной (прямоугольной, треугольной, кусочно-экспоненциальной), для единства подхода к исследованию импульсных САУ используют следующий эффективный метод их математического описания.
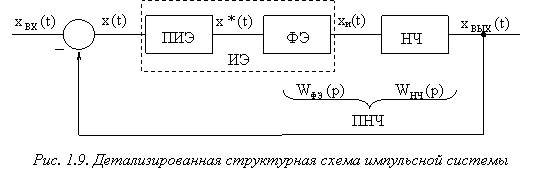
Импульсный элемент, формирующий на выходе последовательность импульсов определенной формы, заменяется последовательно соединенным идеализированным элементом, генерирующим модулированные 
-функции т.е. простейшим импульсным элементом (ПИЭ) или квантователем, и формирующим элементом (ФЭ), преобразующим последовательность -функций в последовательность импульсов заданной формы (рис. 1.9). У модулированной -функции, как и у немодулированной, амплитуда стремится к бесконечности, а длительность – к нулю, при этом площадь импульса, сформированного ПИЭ в момент 
, равна 
, то есть:
. (1.5)
 |
Обозначим передаточную функцию ФЭ как 
, а функцию времени, описывающую импульсы на его выходе, как 
. Тогда, учитывая, что выходной сигнал ФЭ представляет собой реакцию на -функцию, т.е. является функцией веса ФЭ, можно записать:
, (1.6)
где 
– оператор преобразования Лапласа; S(p) – изображение S(t).
Рассмотрим примеры определения передаточных функций ФЭ для двух различных форм импульсов на выходе ИЭ.
Пример 1
Необходимо определить передаточную функцию ФЭ, выходные
импульсы которого имеют прямоуголь
ную форму и скважность 
(рис. 1.10). Такой импульс можно описать следующим образом:
,
где 
– несмещенная и запаздывающая на один интервал квантования (один такт квантования) единичные ступенчатые функции соответственно.
Используя свойство линейности преобразования Лапласа, имеем:
. (1.7)
Формирующий элемент с передаточной функцией (1.7) называется экстраполятором нулевого порядка или фиксатором.
Амплитудно-фазовая характеристика фиксатора:
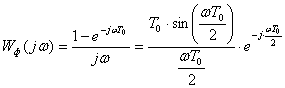. (1.8)
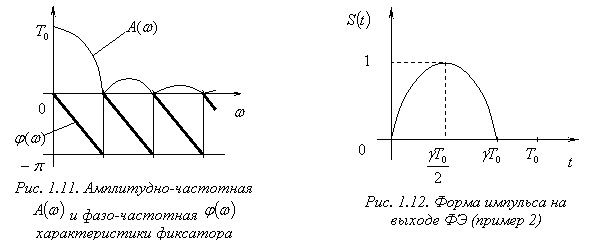
Графики амплитудно-частотной 
и фазо-частотной 
характеристик приведены на рис 1.11.
Формирующий элемент, генерирующий импульсы указанной формы, наиболее часто используется в дискретных САУ. Так, цифро-аналоговые преобразователи, обеспечивающие фиксацию выходного аналогового сигнала на уровне, определенном текущим значением входного цифрового кода, описывается передаточной функцией (1.7).
Пример 2
Необходимо определить передаточную функцию ФЭ, выходные импульсы которого имеют синусоидальную форму (рис. 1.12), описываемую следующим образом:
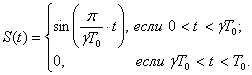
В отличие от функции, рассмотренной в примере 1 функцию S(t) невозможно представить в виде суммы элементарных слагаемых с известными изображениями.
Поэтому для определения 
непосредственно используется формула преобразования Лапласа:
.
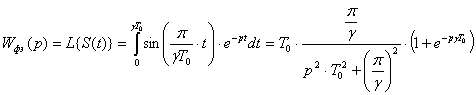Если непрерывная часть системы линейна и имеет передаточную функцию 
, то ФЭ можно отнести к непрерывной части и ввести в рассмотрение приведенную непрерывную часть (ПНЧ), имеющую передаточную функцию:
. (1.9)
При таком подходе дискретность, присущая САУ, определяется исключительно наличием ПИЭ, математическое описание которого не зависит от формы импульса. Выходной сигнал ПНЧ, на вход которой поступают модулированные 
-функции, представляет собой непрерывный сигнал, равный сумме смещенных функции веса ПНЧ:
. (1.10)