Определение. Упорядоченная пара <x, y> интуитивно определяется как совокупность, состоящая из двух элементов х и у, расположенных в определенном порядке. Две пары <x, y>, <u, v> считаются равными тогда и только тогда, когда x=u, y=v.

Упорядоченная n-ка элементов х₁, …, х_n обозначается <x₁, …, x_n>.

Определение. Прямым произведением  множеств X и Y называется множество , элементами которого являются все возможные упорядоченные пары <x, y>, такие, что .

Определение. Прямым произведением  множеств Х₁, Х₂, …, Х_n называется совокупность всех упорядоченных n-ок <x₁, …, x_n> таких, что . Если Х₁=Х₂=…Х_n, то пишут .

Пример 7.

1) Пусть X={1, 2, 3}, Y={0, 1}. Тогда ; .

2) Пусть Х – множество точек отрезка [0, 1], а Y – множество точек отрезка [1, 2]. Тогда  - множество точек квадрата  с вершинами в точках (0, 1), (0, 2), (1, 1), (1,2).

Определение. Бинарным (или двуместным) отношением r называется множество упорядоченных пар.

Если r есть отношение и пара <x, y> принадлежит этому отношению, то наряду с записью <x, y>r употребляется запись xry. Элементы х и у называются координатами (или компонентами) отношения r.

Определение. N-арным отношением называется множество упорядоченных  n-ок.

Определение. Областью определения бинарного отношения r называется множество

Определение. Областью значений бинарного отношения r называется множество

Пусть rXY определено в соответствии с изображением на рис. 1.8 Область определения D_r и область значений E_r определяются соответственно:

D_r={x: (x, y)  r}, E_r={y: (x,y)  r}.

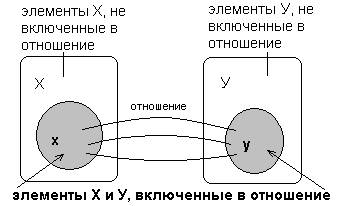
Рис. 1.8. Бинарное отношение

Бинарное отношение можно задать любым из способов задания множеств. Помимо этого отношения, определенные на конечных множествах  обычно задаются:

1) списком (перечислением) пар, для которых это отношение выполняется;

2) матрицей – бинарному отношению соответствует квадратная матрица порядка n, в которой элемент c_ij, стоящий на пересечении i-й строки и j-го столбца, равен 1, если a_i и a_j имеет место отношение, или 0, если оно отсутствует.

Пример 8.

Пусть M={1, 2, 3, 4, 5, 6}. Задать в явном виде (списком) и матрицей отношение r, заданное на множестве , если r  означает «быть строго меньше».

Отношение r как множество содержит все пары элементов a, b из М такие, что a<b. Тогда

r = {(1, 2), (1,3), (1, 4), (1, 5), (1, 6), (2, 3), (2, 4), (2, 5), (2, 6), (3, 4), (3, 5), (3, 6), (4, 5),  (4, 6), (5, 6)}.

Матрица отношения имеет вид:

.

Определение. Бинарное отношение f называется функцией, если из <x, y>f  и <x, z>f следует, что y=z.

Поскольку функции являются бинарными отношениями, то две функции f и g равны, если они состоят из одних и тех же элементов. Область определения функции обозначается D_f, а область значений – R_f. Определяются они так же, как и для бинарных отношений.

Если f – функция, то вместо <x, y>f пишут y=f(x) и говорят, что y – значение, соответствующее аргументу х, или y – образ элемента х при отображении f. При этом х называется прообразом элемента y.

Определение. Назовем f  n-местной функцией из Х в Y если f:Xⁿ®Y. Тогда пишем y=f(x₁, x₂, …, x_n) и говорим, что y – значение функции при значении аргументов x₁, x₂, …, x_n.

Пусть f:X®Y.

Определение. Функция f называется инъективной, если для любых  х₁, х₂, y из y=f(x₁) и  y=f(x₂) следует, что x₁=x₂, то есть каждому значению функции соответствует единственное значение аргумента.

Определение. Функция f называется сюръективной, если для любого элемента yY существует элемент хХ такой, что y=f(x).

Определение. Функция f называется биективной, если f одновременно сюръективна и инъективна.

Рис. 9 иллюстрирует понятия отношения, функции, инъекции, сюръекции и биекции.

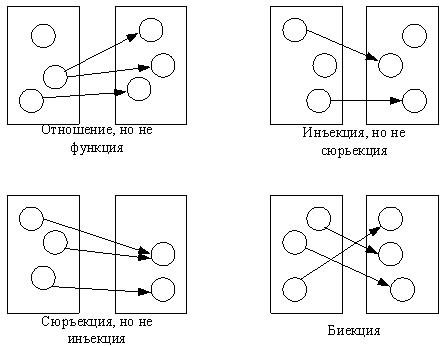
Рис. 1.9. Графическая иллюстрация понятий отношения, инъекции, сюръекции и биекции

Пример 9.

Рассмотрим три функции, заданные на множестве действительных чисел и принимающих значение в этом же множестве:

1) функция f(x)=e^x  — инъективна, но не сюръективна;

2) функция f(x)=x³-x – сюръективна, но не инъективна;

3) функция f(x)=2x+1 – биективна.

Определение. Суперпозиция функций – функция, полученная из системы функций f, f₁, f₂, …, f_k некоторой подстановкой функций f₁, f₂, …, f_k во внешнюю функцию f  вместо переменных и переименованиями переменных.

Пример 10.

Класс элементарных функций есть множество всех суперпозиций так называемых основных элементарных функций (одноместных: степенных, показательных, логарифмических, тригонометрических и обратных тригонометрических) и двуместных функций, представляющих арифметические операции.