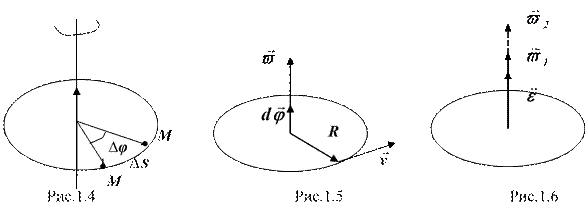
Рассмотрим твердое тело, которое вращается вокруг неподвижной оси. Пусть некоторая точка движется по окружности радиуса  (рис. 1.4). Примем:  – угол поворота за время  . Элементарные (бесконечно малые) углы поворота рассматривают как векторы. Модуль вектора  равен углу поворота, а его направление определяется правилом правого винта.

Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени:

Линейная скорость точки (рис. 1.5) равна:

.,

то есть 

Время, за которое точка совершает один полный оборот; называется периодом вращения:

,

где    – период вращения, с;   – угловая скорость.

Величина, обратная периоду вращения, называется частотой вращения:

,

отсуда угловая скорость равна:.

Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени:

.

Вектор углового ускорения  сонаправлен вектору  при ускоренном движении, при замедленном lдвижении – противонаправлен ему (рис. 1.6).

Связь тангенциальной составляющей ускорения с угловым ускорением описывается формулой: ; нормальной составляющей ускорения – формулой:  .

В случае равнопеременного движения точки по окружности , отсюда: