Коэффициент теплопроводности λ является одной из физических характеристик вещества. Его значение определяют преимущественно экспериментальным путем. Эксперименты показывают, что коэффициент теплопроводности твердых тел зависит от их химического состава и температуры. На рис. 1.9 приведены зависимости λ(θ) для некоторых конструкционных и инструментальных материалов. Из рисунка видно, что температурные зависимости коэффициента теплопроводности имеют достаточно сложный вид. В одних случаях с увеличением θ коэффициент λ снижается, а в других — возрастает, причем темп изменения λ в различных диапазонах температур может быть разным.

Значения коэффициентов теплопроводности приводят обычно в таблицах, либо рассчитывают по формулам, аппроксимирующим результаты экспериментов. Б.Е. Неймарк предложил формулы для расчета коэффициентов теплопроводности углеродистых сталей

и хромоникелевых аустенитных сталей

где ∑ — суммарное содержание всех добавок к железу, включая углерод, %;  m_i – коэффициенты, зависящие от температуры:

Величина  σ представляет собой сумму

где М_j – процентное содержание добавки к железу; А_j – атомный вес элемента, образующего добавку; k – общее количество добавок по рецептуре стали.

1.6. Термическое сопротивление. Тепловые цепи

Формулу   для плоской стенки можно представить в виде

где W – мощность теплового потока, Вт; F – площадь поверхности, через которую передается теплота, м²;   термическое сопротивление стенки, ⁰С/Вт; оно аналогично электрическому сопротивлению R_э=l/γS; здесь l – длина проводника; S – площадь поперечного сечения проводника, материал которого имеет коэффициент теплопроводности γ. Идентичность формул для R и R_э не является случайной, поскольку между процессами распространения тепловой и электрической энергий имеется аналогия. Это позволяет при решении задач, относящихся к теплообмену в системе твердых тел, рассматривать такую систему как тепловую цепь, аналогичную электрической цепи. Тепловые цепи содержат источники и стоки теплоты, а также тепловые связи между твердыми телами, представляемыми в виде термических сопротивлений или емкостей.

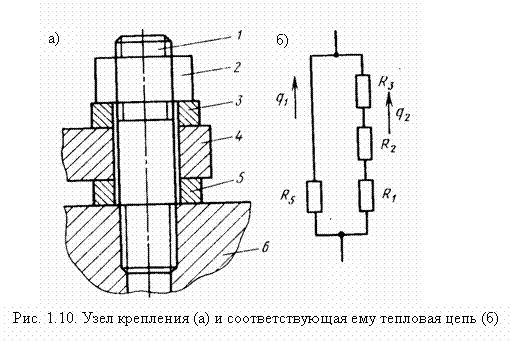
Рассмотрим, например, процесс распространения теплоты в узле крепления, показанном на рис. 1.10, а. Пластина 4 шпилькой 1, гайкой 2 и шайбами 3 и 5 прикреплена к корпусу 6. Корпус в процессе работы машины нагревается до температуры θ₁, и часть теплоты передается в пластину 4. При этом теплота передается по двум маршрутам: от корпуса через шайбу 5 и от корпуса через шпильку 1, гайку 2 и шайбу 3. Изобразим процесс стационарного теплообмена в узле в виде тепловой цепи (рис. 1.10, б). Через R₁- R₅ обозначены термические сопротивления деталей узла тепловым потокам q₁ и q₂, идущим по двум упомянутым выше маршрутам. На основании закона Кирхгофа, который может быть применен как к электрической, так и к тепловой цепи, запишем 

где R – общее сопротивление цепи, R’ и R’’ – термические сопротивления левой и правой ветвей цепи.

При R’=R₅, а R’’=R₁+R₂+R₃   

Далее, можно определить теплоотвод в пластину W, если известна ее средняя температура θ₂. Меняя термические сопротивления элементов цепи (толщину шайб или их материал), можем регулировать теплоотвод в пластину. Это важно, например, когда пластина представляет собой панель для приборов, чувствительных к нагреву.