В данном подразделе мы вводим декартовы произведения, отношения, функции и графы. Изучаем свойства этих математических моделей и связи между ними.

Декартово произведение и перечисление его элементов

Декартовым произведением множеств A и B называется множество, состоящее из упорядоченных пар: A ´ B = {(a,b): (a Î A) & (b Î B)}.

Для множеств A₁, …, A_n декартово произведение определяется по индукции:

.

В случае произвольного множества индексов I декартово произведение  семейства множеств {A_i}_iÎI  определяется как множество, состоящее из таких функций  f: I ®   A_i, что для всех i Î I верно f(i) Î A_i.

Теорема 1

Пусть A и  B – конечные множества. Тогда  | A´B| =  | A|×|B|.

Доказательство

Пусть A = {a₁, …, a_m},  B = {b₁, …, b_n}. Элементы декартового произведения можно расположить с помощью таблицы

(a₁,b₁), (a₁,b₂), …, (a₁,b_n);

(a₂,b₁), (a₂,b₂), …, (a₂,b_n);

…

(a_m,b₁), (a_m,b₂),…, (a_m,b_n),

состоящей из n столбцов, каждый из которых состоит из m элементов. Отсюда |A´B|=mn.

Следствие 1

.

Доказательство

C помощью индукции по n. Пусть формула верна для n. Тогда

Отношения

Пусть n³1 – положительное целое число и A₁, …, A_n – произвольные множества.  Отношением между элементами множеств A₁, …, A_n  или n-арным отношением называется произвольное подмножество .

Бинарные отношения и функции

Бинарным отношением между элементами множеств A и B (или, коротко, между A и B) называется подмножество R Í A´B.

Определение 1

Функцией или отображением называется тройка, состоящая из множеств A и B и подмножества fÍA´B (графика функции), удовлетворяющего следующим двум условиям;

1) для любого x Î A существует такой y Î f, что (x,y) Îf;

2) если (x, y)Îf          и          (x, z) Îf, то y = z.

Легко видеть, что f Í A ´ B будет тогда и только определять функцию, когда для любого x Î A существует единственный y Î f, что (x,y) Î f. Этот y обозначим через f(x).

Функция  называется инъекцией, если для любых x, x’Î A, таких что x¹x’, имеет место f(x) ¹ f(x’). Функция  называется сюръекцией, если для каждого y Î B существует такой x Î A, что  f(x) = y. Если функция является инъекцией и сюръекцией, то она называется биекцией.

Теорема 2

Для того чтобы функция  была биекцией, необходимо и достаточно существования такой функции , что fg = Id_B и gf = Id_A.

Доказательство

Пусть f – биекция. В силу сюръективности f для каждого y Î B можно выбрать элемент x Î A, для которого f(x) = y. В силу инъективности f, этот элемент будет единственным, и мы обозначим его через g(y) = x. Получим функцию .

По построению функции g, имеют место равенства f(g(y)) = y и g(f(x)) = x. Значит, верно fg =Id_B и gf = Id_A. Обратное очевидно: если fg = Id_B и gf = Id_A, то f – сюръекция в силу f(g(y)) = y, для каждого y Î B. В этом случае из  будет следовать , и значит . Следовательно, f – инъекция. Отсюда вытекает, что f – биекция.

Образ и прообраз

Пусть – функция. Образом подмножества X Í A называется подмножество  f(X) = {f(x): xÎX}Í  B.    Для YÍ B  подмножество f^{- -1}(Y) ={xÎA: f(x)ÎY} называется прообразом подмножества Y. 

Отношения и графы

Бинарные отношения можно наглядно показать с помощью ориентированных графов.

Определение 2

Ориентированным графом называется пара множеств (E,V) вместе с парой отображений s,t: E®V. Элементы множества V изображаются точками на плоскости и называются вершинами. Элементы из E называются направленными ребрами или стрелками. Каждый элемент e Î E изображается в виде стрелки (возможно, криволинейной), соединяющей вершину s(e) с вершиной t(e).

Произвольному бинарному отношению R Í V ´ V соответствует ориентированный граф с вершинами v Î V, стрелками которого являются упорядоченные пары (u,v) Î R. Отображения s,t: R®V определяются по формулам:

s(u,v) = u        и         t(u,v) = v.

Пример 1

Пусть V = {1,2,3,4}. Рассмотрим отношение

R = {(1,1), (1,3), (1.4), (2,2), (2,3), (2,4), (3,3), (4,4)}.

Ему будет соответствовать ориентированный граф (рис. 1.2). Стрелками этого граф будут пары (i,j) Î R.

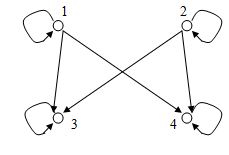
Рис. 1.2. Ориентированный граф бинарного отношения

В полученном ориентированном графе любая пара вершин соединяется не более чем одной стрелкой. Такие ориентированные графы называются простыми. Если не рассматривать направление стрелок, то мы приходим к следующему определению:

Определение 3

Простым (неориентированным) графом G = (V,E) называется пара, состоящая из множества V и множества E, состоящего из некоторых неупорядоченных пар {v₁,v₂} элементов v₁,v₂ Î V таких, что v₁¹v₂.  Эти пары называются ребрами, а элементы из V – вершинами.

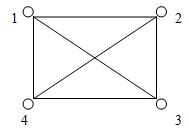
Рис. 1.3. Простой неориентированный граф K₄

Множество E определяет бинарное симметричное антирефлексивное отношение, состоящее из  пар (v₁,v₂), для которых {v₁,v₂} Î E. Вершины простого графа изображаются как точки, а ребра – как отрезки. На рис. 1.3 изображен простой граф с множеством вершин

V = {1, 2, 3, 4}

и множеством ребер

E = {{1,2}, {1,3},{1,4}, {2,3}, {2,4}, {3, 4}}.

Операции над бинарными отношениями

Бинарным отношением между элементами множеств A и B называется произвольное подмножество R Í A ´ B. Запись aRb (при a Î A, b Î  B) означает, что (a,b) Î  R.

Определены следующие операции над отношениями R Í A ´ A:

· R ^-1 = {(a,b): (b,a) ÎR};

· R° S = {(a,b): ($ x Î A)(a,x) ÎR & (x,b) ÎR};

· Rⁿ = R°(R^n-1);

· .

Пусть Id_A = {(a,a): a Î A} – тождественное отношение. Отношение R Í X ´ X называется:

1) рефлексивным, если (a,a) Î R для всех a Î X;

2) антирефлексивным, если (a,a) Ï R для всех a Î X;

3) симметричным, если для всех a, b Î X верна импликация aRb Þ bRa;

4) антисимметричным, если aRb & bRa Þ a=b;

5) транзитивным, если для всех a, b, c Î X верна импликация aRb & bRc Þ aRc;

6) линейным, для всех a, b Î X верна импликация a ¹ b Þ aRb Ú bRa.

Обозначим Id_A через Id. Легко видеть, что имеет место следующее.

Предложение 1

Отношение R Í X ´ X:

1) рефлексивно Û Id Í R;

2) антирефлексивно Û RÇId= Æ;

3) симметрично Û R = R^-1;

4) антисимметрично Û R Ç R^-1 Í Id;

5) транзитивно Û R°RÍ R;

6) линейно Û R ÈId È R^-1 = X ´ X.

Матрица бинарного отношения

Пусть A = {a₁, a₂, …, a_m}       и          B = {b₁, b₂, …, b_n} – конечные множества. Матрицей бинарного отношения R Í A ´ B называется матрица с коэффициентами:

Пусть A – конечное множество, |A| = n       и          B = A. Рассмотрим алгоритм вычисления матрицы композиции T = R°S  отношений R, S Í A ´ A. Обозначим коэффициенты матриц отношений R, S и T соответственно через r_ij, s_ij и t_ij. 

Поскольку свойство (a_i,a_k)ÎT равносильно существованию такого a_j Î A, что (a_i,a_j)ÎR    и          (a_j,a_k) Î S, то коэффициент t_ik будет равен 1, если и только если существует такой индекс j, что  r_ij = 1 и          s_jk = 1. В остальных случаях t_ik равен 0. Следовательно, t_ik = 1 тогда и только тогда, когда .

Отсюда вытекает, что для нахождения матрицы композиции отношений нужно перемножить эти матрицы и в полученном произведении матриц ненулевые коэффициенты заменить на единицы. Следующий пример показывает, как этим способом вычисляется матрица композиции.

Пример 2

Рассмотрим бинарное отношение на A = {1,2,3}, равное R = {(1,2),(2,3)}.  Запишем матрицу отношения R. Согласно определению, она состоит из коэффициентов r₁₂ = 1, r₂₃ = 1 и  остальных r_ij = 0. Отсюда матрица отношения R  равна:

.

Найдем отношение R°R. С этой целью умножим матрицу отношения R на себя:

.

Получаем матрицу отношения:

.

Следовательно, R°R = {(1,2),(1,3),(2,3)}.

Из предложения 1 вытекает следующее следствие.

Следствие 2

Если A = B, то отношение R на A:

1) рефлексивно, если и только если все элементы главной диагонали матрицы отношения R равны 1;

2) антирефлексивно, если и только если все элементы главной диагонали матрицы отношения R равны 0;

3) симметрично, если и только если матрица отношения R симметрична;

4) транзитивно, если и только если каждый коэффициент матрицы отношения R°R не больше соответствующего коэффициента матрицы отношения R.