Определение. Отношение r на множестве Х называется рефлексивным, если для любого элемента хХ выполняется хr х.

Определение. Отношение r на множестве Х называется симметричным, если для любых х, уХ из хr у следует уr х.

Определение. Отношение r на множестве Х называется транзитивным, если для любых х, у, zХ из хr у и уr z следует хr z.

Определение. Рефлексивное, симметричное, транзитивное отношение на множестве Х называется отношением эквивалентности на множестве Х.

Пример 11.

1) Отношение равенства на множестве целых чисел есть отношение эквивалентности.

2) Отношение подобия на множестве треугольников есть отношение эквивалентности.

3) Отношение «строго меньше» на множестве действительных чисел не рефлексивно, не симметрично и транзитивно на этом множестве.

4) Отношение перпендикулярности прямых не рефлексивно, симметрично, не транзитивно.

Пусть r — отношение эквивалентности на множестве Х.

Определение. Классом эквивалентности, порожденным элементом х, называется подмножество множества Х, состоящее из тех элементов yÎY, для которых хrу. Класс эквивалентности, порожденный элементом х, обозначается через [x]:

Определение. Отношение r на множестве Х называется антисимметричным, если для любых х, уХ из хr у  и  уr х следует х=у.

Определение. Рефлексивное, антисимметричное и транзитивное отношение называется отношением частичного порядка на множестве Х.

Пример 12.

1) Отношение «х  у» на множестве действительных чисел есть отношение частичного порядка.

2) Схема организации подчинения в учреждении есть отношение частичного порядка на множестве должностей.

Любое частично упорядоченное множество можно представить в виде схемы, в которой каждый элемент изображается точкой на плоскости, и если у покрывает х, то точки х и у соединяют отрезком, причем точку, соответствующую х, располагают ниже у. Такие схемы называются диаграммами Хассе. На рис. 10 показаны две диаграммы Хассе, причем вторая соответствует линейно упорядоченному множеству.

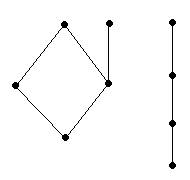
Рис. 1.10. Пример диаграммы Хассе