Абсолютная погрешность дифференцируемой функции y = f(x), вызываемая достаточно малой погрешностью аргу­мента Dx, оценивается величиной :.

Если значения функции f(x) положительны, то для относи­тельной погрешности имеет место оценка:

.

Пример 1

Абсолютные погрешности синуса и косинуса находится по формулам:

D sin x = |cos x|×Dx,

D cos x = |sin x|×Dx, где x изменяется в радианах.

Погрешность вычисления значения функции нескольких переменных (общая формула для погрешности)

Абсолютная погрешность дифференцируемой функции y = f(x₁, x₂, x₃, …, x_n), вызываемая достаточно малыми погрешно­стями Dx₁, Dx₂,…,Dx_n­ аргументов x₁, x₂, x₃,…,x_n, оценивается вели­чиной:

.

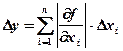Пример 2

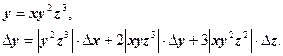
Если значения функции положительны, то для относитель­ной погрешности имеет место оценка:

.

Пример 3

Вычислить значение функции f, абсолютную и от­носительную погрешности вычисления f, если

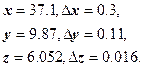
Сначала найдем относительную погрешность вычисления значения f, а затем абсолютную погрешность. Функция f положительна и дифференцируема, поэтому воспользуемся формулой:

;      ;

;

.

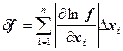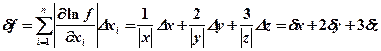Найдем относительные погрешности аргументов:

; .

Относительная погрешность является величиной порядка 1 %, следовательно, значение f содержит 2 верные значащие цифры. Следовательно, в записи f  нужно указать три значащие цифры, две из которых будут верными  и одна сомнительная. Вычислим xy²z³ = 801133.57, оставляя три значащие цифры, получим: f = 801*10³. Зная значение f и её относительную погрешность, найдем абсолютную погрешность:

.