Первая нормальная форма файла

Записью называется конечная последовательность x = (x₁, …, x_n) элементов x_i Î A_i, 1 £ i £ n. Число n называется длиной записи. Для каждого i множество A_i называется доменом i-го атрибута, элемент x_i называется i-м атрибутом или i-й компонентой записи x.

Файлом мы будем называть конечную последовательность записей. База данных состоит из файлов, связанных между собой некоторыми условиями.

Определение 1

Файл находится в первой нормальной форме (1NF), если для него задано   некоторое положительное целое число n и последовательность множеств (A₁, ×××, A_n) таких, что

· файл состоит из записей (x₁, …, x_n) Î A₁ ´ …´ A_n;

· среди этих записей (x₁, …, x_n) Î A₁ ´ … ´ A_n нет одинаковых.

Пример 1

Записи файла расположим в таблице 1.2. В первой строке этой таблицы будут выписаны имена, обозначающие домены атрибутов. Эти имена мы будем называть атрибутами.

Таблица 1.2 Пример набора записей

Вуз	Номер зачетной книжки	Фамилия, имя, отчество (ФИО)	Год поступления
АмГПГУ	10802	Иванов Павел Сергеевич	2010
КнАГТУ	10802	Петрова Галина Сергеевна	2010

Данная таблица содержит две записи. Эти записи отличаются значениями первого и третьего атрибутов. Стало быть, файл, состоящий из этих записей, находится в первой нормальной форме.

Замечание

Мы видим, что записи в файле являются в точности элементами декартового  произведения доменов атрибутов. Если файл находится в первой нормальной форме, то он является упорядоченным набором различных записей. В этом случае файл определяет отношение, состоящее из этих записей.

Вторая нормальная форма

Рассмотрим файл, находящийся в первой нормальной форме. Его записи

x = (x₁, …, x_n) Î A₁ ´ A₂ ´ … ´ A_n

будут составлять некоторое отношение

R Í A₁ ´A₂ ´ … ´A_n.

Файл будет состоять из всех элементов множества R.

Определение 2

1) атрибут A_k функционально зависит от множества атрибутов , если для любых элементов x, y Î R Í A₁ ´ A₂ ´ … ´ A_n из равенства их компонент  следует равенство ;

если атрибут A_k функционально зависит от множества атрибутов , но не зависит функционально ни от какого  строго содержащегося в нем

1) подмножества , то A_k называется функционально полно зависящим от множества атрибутов ;

2) множество атрибутов   называется ключом записи файла, если, во-первых, для всех k Î {1, 2, …, n} атрибуты A_k функционально зависят от , и, во-вторых, это множество атрибутов удовлетворяет условию минимальности, в том смысле, что для любого подмножества множества   некоторый атрибут A_k  не зависит функционально от атрибутов этого подмножества. Во множестве всех ключей можно отметить некоторые ключи. Эти ключи называются выделенными. Остальные – невыделенными;

3) первичным ключом называется произвольный выделенный ключ. Ключ, не являющийся первичным, называется возможным.

Определение 3

Файл с первичным ключом   находится во второй нормальной форме (2NF), если он находится в первой нормальной форме, и для любого  атрибут A_k функционально полно зависит от атрибутов .

Поскольку множество записей для файла в первой нормальной форме совпадает с отношением, определенном этим файлом, то можно говорить о второй нормальной форме отношения.

Пример 2

Определим первичный ключ (см. табл. 1.2) как множество атрибутов {Вуз, Номер зачетной книжки}. Год поступления  зависит от номера зачетной книжки. Поэтому зависимость года поступления от первичного ключа не является функционально полной. Стало быть, файл не находится во второй нормальной форме.

Таблица 1.3 Первый файл разбиения

Вуз	Номер зачетной книжки	ФИО
АмГПГУ	10802	Иванов Павел Сергеевич
КнАГТУ	10802	Петрова Галина Сергеевна

Разобьем этот файл на два файла (табл. 1.3, 1.4), находящиеся во второй нормальной форме. Первый файл (табл. 1.3) не будет содержать года поступления, второй (табл. 1.4) содержит номер зачетной книжки и год поступления. Он состоит из одной записи.

Таблица 1.4 Второй файл разбиения

Номер зачетной книжки	Год поступления
10802	2010

Третья нормальная форма

Определение 4

Атрибут A_k транзитивно зависит от множества атрибутов , если существует множество, состоящее из атрибутов , каждый из которых

функционально зависит от , такое,  что A_k функционально зависит от .

Определение 5

Файл с первичным ключом   находится в третьей  нормальной форме (3NF), если он находится в первой нормальной форме, и для любого  функциональная зависимость атрибута A_k от атрибутов  не является  транзитивной.

Произвольный ключ отношения можно выделить как первичный. Если с помощью выделения любого ключа как первичного мы получаем отношение, находящееся в третьей нормальной форме, то заданное отношение называется находящимся в нормальной форме Бойса-Кодда. В частности, отношение будет находиться в нормальной форме Бойса-Кодда, если оно допускает единственный ключ.

Упражнения

3. Задано подмножество A Í U. Найти все подмножества   X Í U,  для которых

A Ç X = Æ.

4. Решить систему уравнений:

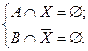
5. Решить уравнения;

1) ;

2) ;

3) ;

4) .

6. Пусть  – множество всех функций B ® A. Установить биекции между множествами:

1) A ´ B              и          B ´ A;

2) (A ´ B)^С          и          A^C ´ B^C;

3) (A^B)^C               и          A^B´C;

4) A^BÈC                и          A^B ´ A^C,          если B Ç C = Æ.

7. Построить бинарное отношение:

1) рефлексивное, симметричное, не транзитивное;

2) рефлексивное, антисимметричное, не транзитивное;

3) рефлексивное, транзитивное, не симметричное;

4) антисимметричное, транзитивное, не рефлексивное.

8. Доказать, что пересечение семейства отношений эквивалентности на заданном множестве является отношением эквивалентности.

9. Построить пример частично упорядоченного множества, имеющего ровно один минимальный элемент, но не имеющего наименьшего элемента.

3. Доказать, что если R – отношение порядка, то R^-1 – отношение порядка.

4. Доказать, что пересечение отношений порядка является отношением порядка. Всегда ли объединение отношений порядка является отношением порядка?

5. Найти число рефлексивных отношений на множестве из n элементов.

6. Найти число симметричных отношений на множестве из n элементов.      

7. Будет ли множество функций X ® R решеткой относительно отношения порядка:

f£g Û   f(a) £g(a)?

8. Сколько подмножеств множества A = {1,2, …,300} содержат, по крайней мере, одно число, кратное 5, и ни одного, кратного 10?

9. Сколько подмножеств множества A = {1,2,…,300} не содержат ни  чисел, кратных 4, ни чисел, кратных 6?

10. Сколько подмножеств множества A = {1,2,…,300} состоят из чисел, кратных 4, но не содержат чисел, кратных 6?

11. Сколько подмножеств множества A = {1,2,…,300} состоят из чисел, кратных 4, и сверх того содержат, по крайней мере, одно число, кратное 6?