Математическое описание температурных полей  в  компонентах технологических систем, как, впрочем, и в любых других твердых телах, выполняется с помощью дифференциального уравнения  теплопроводности. Выведем это уравнение при следующих допущениях:

1) твердое тело однородно и изотропно;

2) в  процессе теплопередачи не происходят фазовые превращения;

3) деформация, вызванная изменением температуры, пренебрежимо мала по сравнению с размерами тела.

Выделим из нагретого тела элементарный объем на основании закона сохранения энергии:

,

где dQ — общее изменение внутренней энергии вещества в  объеме за время; - количество теплоты, поступившей в этот объем путем теплопро

водности; - количество теплоты, возникшее в объеме в связи с функционированием в нем внутренних источников.

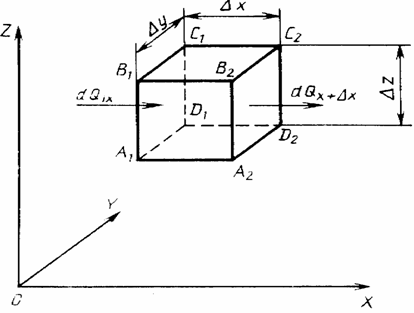
Рис. 14. Схема к выводу дифференциального уравнения теплопроводности

Можно получить для определения количества теплоты, поступающей в объем  по направлению OY и OZ .

.

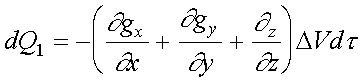Теперь определим величину . Если объемную плотность тепловыделения внутренних источников обозначим  , Вт/м³, то за время dв объеме  накопится теплота:

.

Величина , стоящая в левой части уравнения , может быть найдена из выражения:

,

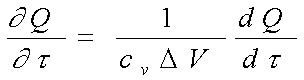где: С_v — объемная теплоемкость вещества Дж/(м с);

С_g - массовая теплоемкость Дж/(кг с).