Система является очень сложным механизмом для понимания. Если нужно понять какие-то взаимосвязи в системе, то необходимо упростить систему, не искажая ее. Для этих целей применяют моделирование, т.е. представляют изучаемую систему в виде такой модели, которая позволит понять, в какой среде приходится жить, работать и отдыхать человеку и оценить уровень нагрузки на человека от факторов среды обитания. Кроме этого, модель должна позволить следить за изменением уровня нагрузки на человека при изменении качественной и количественной характеристики факторов среды.

Для того чтобы перейти к моделированию, необходимо сначала представить место человека в системе, это можно сделать схематично. Схема представлена на рис. 10.1.

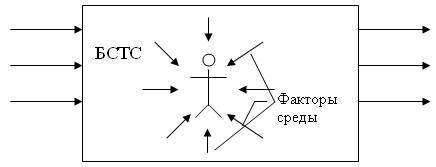
Рис. 10.1. Схема положения человека в БСТС

Человек является одним из элементов БСТС. Система состоит из четырех равнозначных элементов: природы, техносферы. социума и человека. Состояние устойчивого равновесия системы может зависеть в равной степени от состояния всех четырех компонентов. Но на практике чаще всего бывает, что состояние устойчивого равновесия системы зависит от самого слабого элемента системы. В нашем случае таким элементом является человек. Поэтому мы выделяем человека внутри системы и рассматриваем его во взаимодействии со средой, которую формируют оставшиеся элементы: техносфера, природа и социум. Схема такого взаимодействия представлена на рис. 10.2.

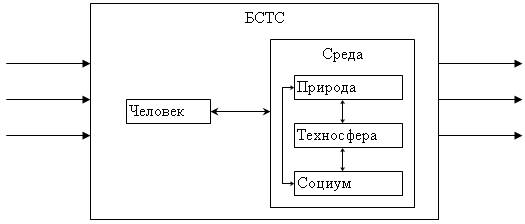
Рис. 10.2. Классическая схема изучения систем «человек-среда»

Таким образом, осуществлен переход к классической (упрощенной) схеме представления крупных систем, которая называется «человек-среда».

Но среда в таких БСТС, как город, имеет свои особенности. Человек в городе находится на улице (ее еще называют окружающей средой или макросредой), на производстве (производственная среда) и дома (бытовая среда или микросреда). Таким образом, среда в БСТС – это суперпозиция трех сред: окружающей; бытовой и производственной.

Классическая модель представления системы модифицировалась и представляет собой модель, представленную на рис. 10.3.

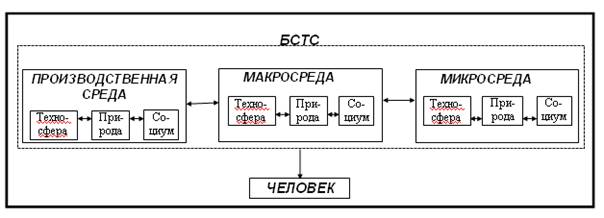
Рис. 10.3. Вариант представления классической модели БСТС