Аналогами начальных и делительных цилиндров цилиндрических передач в конических передачах являются начальные и делительные конусы с углами ![]() и
и ![]() (рис. 10.4). При коэффициентах смещения инструмента
(рис. 10.4). При коэффициентах смещения инструмента ![]() начальные и делительные конусы совпадают.
начальные и делительные конусы совпадают.
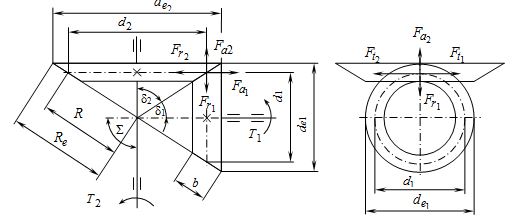
Рис. 10.4. Геометрические и силовые параметры конического зубчатого зацепления
![]()
 Важнейшим геометрическим параметром конической передачи является внешнее конусное расстояние (
Важнейшим геометрическим параметром конической передачи является внешнее конусное расстояние (![]() ). По смыслу оно подобно межосевому расстоянию (
). По смыслу оно подобно межосевому расстоянию (![]() )цилиндрической передачи. Между внешними делительными диаметрами
)цилиндрической передачи. Между внешними делительными диаметрами ![]() и
и ![]() (рис.10.4) и внешним конусным расстоянием существует следующая зависимость:
(рис.10.4) и внешним конусным расстоянием существует следующая зависимость:
![]() .
.
Внешний делительный диаметр колеса (![]() ) стандартизирован, определяется из условия прочности по контактным напряжениям.
) стандартизирован, определяется из условия прочности по контактным напряжениям.
Кроме размеров по внешнему торцу конуса, удобных для измерения и указываемых на чертежах, различают также размеры в среднем сечении (посередине ширины зубчатого венца ![]() ). Данные размеры используются при силовых расчетах. Между средним (R) и внешним (
). Данные размеры используются при силовых расчетах. Между средним (R) и внешним (![]() ) конусными расстояниями существует зависимость:
) конусными расстояниями существует зависимость:
![]() .
.
Средние делительные диаметры конических зубчатых колес определяются по формуле:
![]() ,
,
смещения ![]() определяют в зависимости от эквивалентного числа зубьев (
определяют в зависимости от эквивалентного числа зубьев (![]() ) и передаточного числа (u) по ГОСТ 19624-74 и ГОСТ 19326-73, или по формуле ЭНИМС:
) и передаточного числа (u) по ГОСТ 19624-74 и ГОСТ 19326-73, или по формуле ЭНИМС:
![]() ,
,
где х – для прямозубой передачи; хn – для передачи с круговыми зубьями.
Для конических передач при u ≥ 2,5 рекомендуется применять тангенциальную коррекцию, заключающуюся в утолщении зуба шестерни и соответствующем утончении зуба колеса. Как правило, для конических зубчатых передач применяют высотную коррекцию в сочетании с тангенциальной коррекцией. Применение высотной коррекции повышает износостойкость и сопротивление зубьев заеданию, тангенциальная коррекция выравнивает прочность зубьев шестерни и колеса.
Пример расчета геометрических параметров (рис. 10.5) конической ортогональной передачи с прямыми зубьями приведен в табл. 10.3.
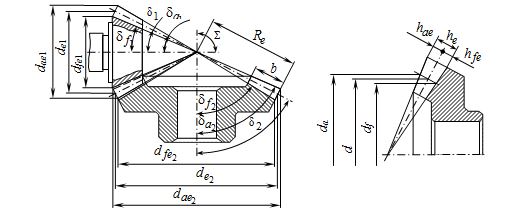
Рис. 10.5. Геометрические параметры конической зубчатой передачи
Таблица 10.3 Расчет геометрических параметров конической передачи
|
Параметры и обозначения |
Формулы |
Значения |
||
|
Исходные данные |
Число зубьев |
|
– |
15 |
|
|
– |
30 |
||
|
Внешний окружной модуль |
|
– |
5 |
|
|
Число зубьев плоского колеса, |
|
33,5410 |
||
|
Внешнее конусное расстояние |
|
83, 8525 |
||
|
Ширина зубчатого венца b, мм |
|
25, 1558 |
||
|
Принятая ширина зубчатого венца b, мм |
по ГОСТ 12289-76 |
25 |
||
|
Среднее конусное расстояние R, мм |
|
71,3525 |
||
|
Средний окружной модуль |
|
4,2546 |
||
|
Внутренний окружной модуль |
|
3,5093 |
||
|
Средний делительный диаметр d, мм: |
||||
|
шестерни |
|
63,8197 |
||
|
колеса |
|
127,6393 |
||
|
Передаточное число u |
|
2 |
||
|
Угол делительного конуса, град: |
||||
|
колеса |
|
63,4349 |
||
|
|
||||
|
шестерни |
|
26,5651 |
||
|
|
||||
|
Коэффициент смещения шестерни |
|
0,39 |
||
|
Коэффициент изменения толщины зуба шестерни |
Вводится при |
0 |
||
|
Внешняя высота головки зуба |
|
6,9365 |
||
|
|
3,0635 |
|||
Продолжение табл. 10.3
|
Параметры и обозначения |
Формулы |
Значения |
|
Внешняя высота головки зуба |
|
6,9365 |
|
|
3,0635 |
|
|
Внешняя высота ножки зуба |
|
4,0635 |
|
|
7,9365 |
|
|
Внешняя высота зуба |
|
11,0000 |
|
|
11,0000 |
|
|
Внешняя окружная толщина зуба |
|
9,2636 |
|
|
6,4443 |
|
|
Угол ножки зуба |
|
2,7744 |
|
|
||
|
|
5,4068 |
|
|
|
||
|
Угол конуса вершин |
|
31,9719 |
|
|
||
|
|
66,2093 |
|
|
|
||
|
Угол конуса впадин |
|
23,7907 |
|
|
||
|
|
58,0281 |
|
|
|
||
|
Внешний делительный диаметр |
|
75 |
|
|
150 |
|
|
Внешний диаметр вершин зубьев |
|
87,4084 |
|
|
152,7401 |
|
|
Внешний диаметр впадин зубьев |
|
67,7674 |
|
|
134,5742 |
|
|
Расстояние от вершины до плоскости внешней окружности вершин зубьев B, мм |
|
71,8979 |
|
|
34,7599 |