1) Если ![]() , то
, то ![]() — неопределённый интеграл, то есть
— неопределённый интеграл, то есть ![]() .
.
2) Основные свойства неопределённого интеграла:
а) ![]() ;
; ![]() ;
;
б) ![]() ;
;
в) ![]() ,
, ![]() — постоянная;
— постоянная;
г) ![]() .
.
3) Таблицы простейших неопределённых интегралов
![]() .
. ![]() .
.
![]() .
. ![]() .
.
![]() .
. ![]() .
.
![]() .
. ![]() .
.
![]() .
. ![]() .
.
![]() .
. ![]() .
.
![]() .
. ![]() .
.
![]() .
. ![]() .
.
![]() .
.
4) Наиболее важные методы интегрирования:
а) метод разложения (непосредственного интегрирования);
б) метод замены (подстановки);
в) метод интегрирования по частям;
г) интегрирование простейших дробей и дробно-рациональных функций;
д) интегрирование тригонометрических выражений;
е) интегрирование простейших иррациональностей.
Объяснения.
а) метод разложения или непосредственного интегрирования:
![]() , где
, где ![]() .
.
Пример 44. Найти ![]() .
.
Решение: ![]() =
=
![]() .
.
Пример 45. Найти ![]() .
.
Пример 46. Найти ![]() .
.
Решение: ![]() .
.
Пример 47. Найти ![]() .
.
Решение: ![]() .
.
б) метод подстановки (введение новой переменной):
![]() ,
,
где ![]() - непрерывно дифференцируемая, монотонная функция переменной t.
- непрерывно дифференцируемая, монотонная функция переменной t.
Пример 48. Найти ![]() .
.
Решение: Делаем замену ![]() ,
, ![]() ,
,
тогда ![]() ,
,
но t = 5x, поэтому делаем возврат к старой переменной:
![]() .
.
Пример 49. Найти ![]() .
.
Решение: Делаем замену ![]() (подстановка Эйлера), где t – новая переменная. Перепишем это равенство так:
(подстановка Эйлера), где t – новая переменная. Перепишем это равенство так:
![]() ,
,
найдём
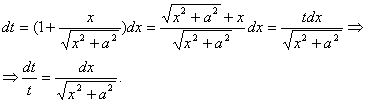
Откуда ![]() .
.
Таким образом, ![]()
в) метод интегрирования по частям:
![]() ,
,
где u = u(x), v = v(x) – непрерывно дифференцируемые функции.
Пример 50. Найти ![]() .
.
![]()
![]() Решение:
Решение: 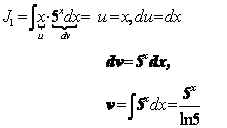
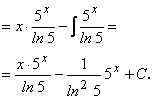
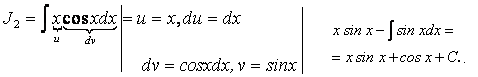
г) интегрирование простейших дробей и рациональных функций:
![]() где
где 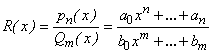 .
.
Нахождение таких интегралов основано на разложении рациональной дроби на сумму простейших дробей вида:
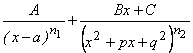 ,
,
где n1 и n2 – натуральные числа; a, A, B, C, p, q – действительные числа; ![]() (корни трёхчлена
(корни трёхчлена ![]() — комплексные).
— комплексные).
Пример 51. Найти: ![]() .
.
Решение:
1) приравняем знаменатель нулю, найдём его корни: х1=2, х2=3,
2) дробь:
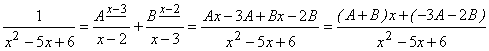 ;
;
|
тогда ![]() .
.
Следовательно,
![]() .
.
Или ![]() ;
;
![]() .
.
1) Найдём корни знаменателя, для чего
![]() .
.
2) Разложим подынтегральную функцию на сумму простейших дробей:
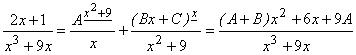 ;
;
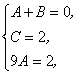
![]() .
.
3)  ;
;
4) ![]() .
.
д) интегрирование тригонометрических выражений проводится с использованием тригонометрических формул:
а) ![]() .
.
б) ![]() .
.
в) ![]() .
.
Неопределённые интегралы вида ![]() , где
, где ![]() находят с помощью формул:
находят с помощью формул:
![]() ,
,
если m и n – чётные; если среди m и n есть нечётные, то от нечётной степени отделяют множитель и вводится новая переменная.
Неопределённый интеграл вида ![]() , где R – рациональная функция от sin х и cos х, введением универсальной подстановки
, где R – рациональная функция от sin х и cos х, введением универсальной подстановки ![]() приводится к интегралу
приводится к интегралу ![]() от рациональной функции.
от рациональной функции.
Примеры 52. ![]()
Решения:
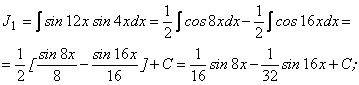
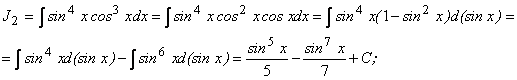
![]()
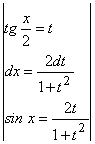 =
=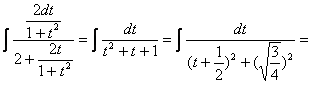
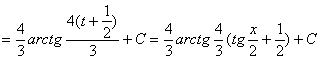 .
.
е) интегрирование простейших иррациональностей можно проводить с использованием метода замены переменной с помощью тригонометрических подстановок, гиперболических и других.
Примеры 53. ![]()
Решения:
![]()
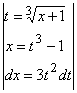 =
=![]() ;
;
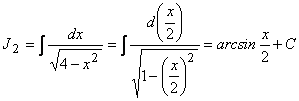 ;
;
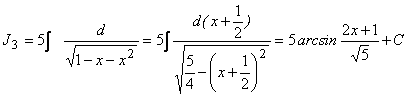 .
.
5) Формула Ньютона-Лейбница: если f(x) – непрерывна на [a, b] и ![]() , то
, то
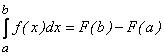 .
.
6) Основные свойства определённого интеграла:
а)  ;
;
б)  ;
;
в)  ;
;
г) 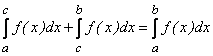 ;
;
д) 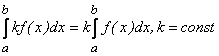 ;
;
е) 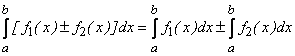 ;
;
ж)  ,
, 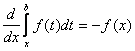 , (везде рассматриваемые функции непрерывны).
, (везде рассматриваемые функции непрерывны).
7) Теорема о среднем: если f(x) – непрерывна на [a, b], то
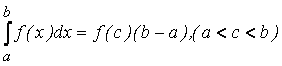 .
.
8) Формула интегрирования по частям в определённом интеграле:
 .
.
9) Формула замены переменной в определённом интеграле:
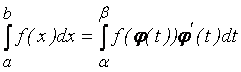 ,
,
где ![]()
10) Формула трапеций:
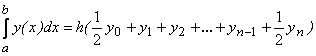 ,
,
где ![]() .
.
11) Формула Симпсона
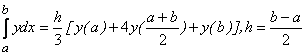 .
.
12) Несобственный интеграл первого рода:
 .
.
13) Несобственный интеграл от неограниченных функций:
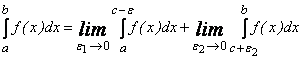 ,
,
где ![]() – точка разрыва второго рода.
– точка разрыва второго рода.
Пример 54. Найти: 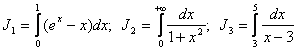 .
.
Решения:
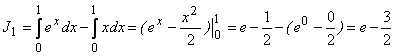 ;
;
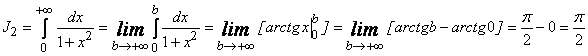 .
.
Значит, данный интеграл сходится.
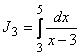 : подынтегральная функция
: подынтегральная функция ![]() терпит бесконечный разрыв при х = 3, следовательно, используя формулу для нахождения несобственного интеграла от неограниченной функции, будем иметь:
терпит бесконечный разрыв при х = 3, следовательно, используя формулу для нахождения несобственного интеграла от неограниченной функции, будем иметь:
Следовательно, данный интеграл расходится.
14) Площадь криволинейной трапеции, ограниченной непрерывной линией y = f(x) (![]() ), осью Ох и двумя ординатами f(a) и f(b) (a < b):
), осью Ох и двумя ординатами f(a) и f(b) (a < b):
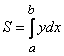 .
.
15) Площадь сектора, ограниченного непрерывной линией ![]() (
(![]() и
и ![]() — полярные координаты) и лучами
— полярные координаты) и лучами ![]() :
:
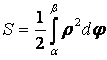 .
.
16) Длина дуги гладкой кривой y = f(x), ![]() :
:
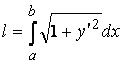 .
.
17) Длина дуги в полярных координатах:
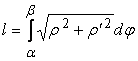 .
.
18) Длина дуги, заданной параметрически (![]() ):
):
 .
.
19) Объем тела с известным поперечным сечением S(x):
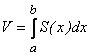 .
.
20) Объем тела вращения:
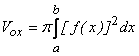 — вокруг оси OX;
— вокруг оси OX;
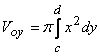 — вокруг оси ОУ .
— вокруг оси ОУ .
21) Площадь поверхности вращения:
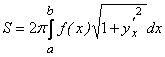 .
.
22) Работа переменной силы F = F(x) на участке ![]()
![]() :
:
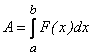 .
.
Пример 55: Найти площадь фигуры, ограниченной линией ![]() .
.
Решение: Площадь криволинейной трапеции будет:
![]() .
.
Пример 56: Вычислить площадь фигуры, ограниченной эллипсом:
![]() .
.
Решение: фигура симметрична, следовательно, используя параметрическое задание, найдем:
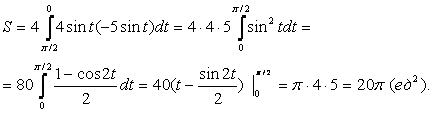
Пример 57: Вычислить площадь фигуры, ограниченной лемнискатой ![]() (см. рис. 5.1, в).
(см. рис. 5.1, в).
Решение: Фигура симметрична относительно своей оси, по формуле площади в полярных координатах получим:
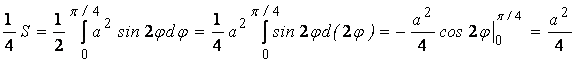 .
.
Таким образом, ![]() .
.
Пример 58: Вычислить длину дуги винтовой линии:
![]() .
.
Решение:
![]() ,
,
тогда 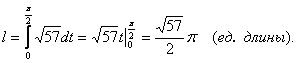
Пример 59: Вычислить длину кардиоиды ![]() .
.
Решение: Найдем

Пример 60: Вычислить площадь поверхности, образованной вращением вокруг оси ОХ линии ![]() .
.
Решение:
![]() так как
так как ![]() .
.
По формуле поверхности вращения получаем:

Пример 61: Вычислить объем тела, полученного вращением вокруг оси ОХ фигуры, ограниченной линией ![]() , у = 0, х = 5.
, у = 0, х = 5.
Решение: Найдем ![]() , тогда по формуле для объема вращения получим:
, тогда по формуле для объема вращения получим:
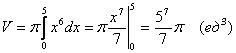 .
.