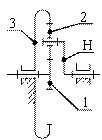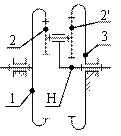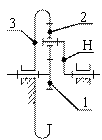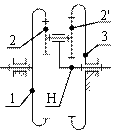Основной характеристикой планетарной передачи является передаточное отношение (u). Передаточное отношение может быть выражено через отношение чисел зубьев (z), угловых скоростей (ω), частот вращения (n). Существуют аналитический и графический методы кинематического исследования передачи.

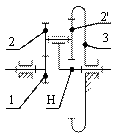
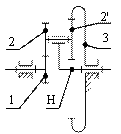
Сущность аналитического метода состоит в следующем. Пусть требуется определить передаточное отношение () от центрального колеса 1 к водилу Н при неподвижном центральном колесе 3 для планетарного механизма (рис. 12.6, а, б).

Аналитический метод (метод инверсии) определения передаточного отношения основан на принципе обращения движения, который впервые предложил Виллис. Суть метода заключается в следующем: всему механизму придается угловая скорость , в результате чего водило Н останавливается, а колесо 3 начинает вращаться с угловой скоростью . Звенья обращенного механизма (рис. 12.6, в) будут вращаться с угловыми скоростями:

;      ;      ,

где , ,  – угловые скорости, соответственно, звеньев 1, 2 и 3 при остановленном водиле Н (надстрочный индекс указывает на условную неподвижность соответствующего звена).

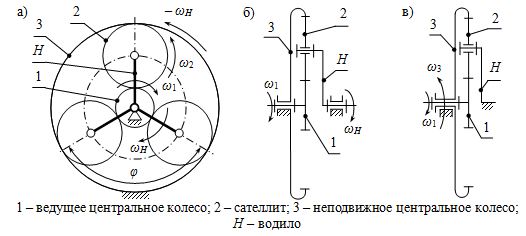
Рис. 12.6. Планетарный (а, б) и обращенный (в) механизмы

Определим передаточное отношение  обращенного механизма (рис. 12.6, в) при ведущем звене 1 и выходном звене 3:

,

откуда найдем передаточное отношение рассматриваемого планетарного механизма:

. (12.1)

При ведущем центральном колесе 3 и неподвижном центральном колесе 1 передаточное отношение планетарного механизма определяется по аналогичной формуле:

. (12.2)

Формулы (12.1) и (12.2) используется для определения передаточного отношения планетарных механизмов при ведущем центральном колесе и выходном водиле Н. При ведущем водиле Н формулы (10.1) и (10.2) приводятся к виду:

;             .  (12.3)

Теперь определим передаточные отношения рассматриваемого планетарного механизма через числа зубьев колес ():

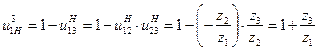;  (12.4)

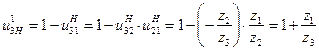;   (12.5)

;         .  (12.6)

При определении передаточного отношения планетарного механизма необходимо помнить, что при внешнем зацеплении (зубчатые колеса 1 и 2) знак передаточного отношения отрицательный (так как зубчатые колеса 1 и 2 вращаются в противоположных направлениях), при внутреннем зацеплении (зубчатые колеса 2 и 3) – положительный (зубчатые колеса вращаются в одинаковом направлении).

Пользуясь формулами (12.1) – (12.6), можно аналитически определить угловую скорость любого звена механизма. Найдем, например, угловую скорость  сателлита 2. Для этого составим передаточное отношение:

,

откуда имеем

.

Для других простейших схем планетарных механизмов передаточные отношения приведены в табл. 12.1.

Таблица 12.1 Характеристики планетарных передач

Продолжение табл. 12.1