К наиболее употребительным при экспертном оценива­нии методам измерений относятся ранжирование, пар­ное сравнение, непосредственная оценка, последователь­ное сравнение.

При описании каждого из перечисленных методов будет предполагаться, что имеется конечное число измеря­емых объектов О₁, …, О_n и сформулирован    один или совокупность показателей  (признаков)  сравнения I₁, …, I_k, по которым осуществляется сравнение объектов. Сле­довательно, методы измерения будут различаться лишь процедурой сравнения объектов. Эта процедура включа­ет построение отношений между объектами эмпириче­ской системы, выбор функции f, отображающей объекты эмпирической системы на числовую систему, и опреде­ление типа шкалы измерений. Рассмотрим все эти воп­росы для каждого метода измерения.

Ранжирование

Ранжирование представляет собой процедуру упоря­дочения объектов, выполняемую экспертом. На основе своих знаний и опыта эксперт располагает объекты в порядке предпочтения, руководствуясь одним или не­сколькими показателями сравнения. В зависимости от вида отношений между объектами возможны различные варианты упорядочения объектов. Рассмотрим эти вари­анты.

Пусть среди объектов нет одинаковых по сравнивае­мым показателям т.е. нет эквивалентных объектов. В этом случае между объектами существует только отношение строгого порядка, обладающего свойствами:

· несимметричности (если О_i  O_j, то О_j p O_i);

· транзитивности (если О_i  O_j, О_j  O_k,то О_i  O_k);

· связности (для любых двух объектов, либо О_i  O_j, либо О_j  O_i).

В результате сравнения всех объектов по отношению строгого порядка эксперт составляет упорядоченную по­следовательность:

О₁  O₂ … O_n,   (12.2)

где объект с первым номером является наиболее пред­почтительным из всех объектов, объект со вторым номе­ром менее предпочтителен, чем первый объект, но пред­почтительнее всех остальных и т.д.

Полученная система с отношением порядка <О₁ O₂ > образует серию. Для серии

доказано существование чис­ловой системы, элементами которой являются числа, а отношение порядка  есть отношение «больше чем» или «меньше чем». Это означает, что существует число­вое представление f(O_i), такое, что последовательности (12.2) соответствует последовательность чисел:

f(О_l) > f(О₂) >…> f(О_n),   (12.3)

или обратная последовательность

f(О_l) < f(О₂) <…< f(О_n).   (12.4)

Соответствие последовательности (12.3) и (12.4), т.е. их изоморфизм или гомоморфизм, можно определить, вы­бирая любые числовые представления. Единственным ограничением является монотонность преобразования. Следовательно, допустимое преобразование при перехо­де от одного числового представления к другому долж­но обладать свойством монотонности. Но таким свойст­вом обладает шкала порядков. Таким образом, ранжирование объектов производится в шкале порядков.

В практике экспертного ранжирования чаще всего применяется числовое представление последовательно­сти  в виде натуральных чисел:

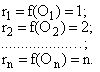   (12.5)

Числа r_1, r_2, …, r_n называются рангами. Наиболее пред­почтительному объекту присваивается первый ранг, второму – второй ранг и т.д.

Пусть теперь среди объектов могут быть эквивалент­ные. Это означает, что, кроме отношения строгого порядка, между некоторыми объектами возможно отношение эквивалентности. В результате ранжирования при наличии отношений порядка и эквивалентности эксперт составляет упорядо­ченную последовательность, в которой некоторые объек­ты могут быть эквивалентными. Например, упорядоче­ние может иметь вид:

O₁  O₂  O₃  O₄ O₅ … O_n-1  O_n.   (12.6)

В последовательности (12.6) объекты О₃, О₄, О₅ эквивалентны между собой, а объекты О_n-1, О_п – между собой.

Система с отношениями эквивалентности и порядка образует квазисерию. Для квазисерии существует числовая система с отношениями «больше чем» («меньше чем») и «равно». Любые две числовые системы для квазисерии связаны между собой монотонным преобразованием. Следовательно, и в этом случае для ранжирования

объектов используется шкала порядков. Таким образом, ранжирование всегда проводится. в .шкале порядка независимо от того, имеются ли среди объектов эквивалентные или нет.

В практике ранжирование объектов, между которыми допускаются как отношения строгого порядка, так и эквивалентности, числовое представление выбирается следующим образом. Наиболее предпочтительному объекту присваивается ранг, равный единице, второму по предпочтению – второй ранг и т.д. Для эквивалентных объектов удобно назначать одинаковые ранги, равные среднему арифметическому значению рангов, присваиваемых одинаковым объектам. Такие ранги называют связанными рангами. Для примера упорядочения  при n = 10 ранги объектов O₃, O₄, O₅ будут одинаковыми и равными:

r₃ = r₄ = r₅ =  = 4.

В этом же примере ранги объектов O₉ и O₁₀ также одинаковы и равны среднему арифметическому:

r₉ = r₁₀=  = 9,5.

Как следует из этого примера, связанные ранги могут ока­заться дробными числами.

Удобство использования связанных рангов заключается в том, что сумма рангов (n) объектов равна сумме натуральных числе от единицы до n. При этом любые комбинации связанных рангов не изменяют эту сумму. Это обстоятельство существенно упрощает обработку результатов ранжирования при групповой экспертной оценке.

При групповой экспертной оценке каждый i-й эксперт присваивает каждому объекту j ранг r_ij. В результате проведения экспертного оценивания получается матрица рангов ||r_ij|| размерности n× m, где m – число экспертов (I = l, …, m), а n – число объектов (j = 1,…, n).

Напомним, что ранги объектов определяют только порядок расположения объектов по показателям сравнения. Ранги как числа не дают возможности сделать вывод о том, на сколько или во сколько предпочтительнее один объект по сравнению с другим. Если, например, ранг объекта равен трем, то отсюда не следует делать вывод о том, что объект, имеющий ранг, равный единице, в три раза предпочтительнее, чем объект, имеющий ранг, равный трем.

Достоинством ранжирования как метода измерения является простота осуществления процедур. Как показывает опыт, при числе объектов, большем 15—20, эксперты затрудняются в построении ранжированного ряда. Это объясняется тем, что в процессе ранжирования эксперт должен установить взаимосвязи между всеми объектами, рассматривая их как единую совокупность. При увеличении числа объектов количество связей между ними растет очень быстро. Удержание и анализ большой совокупности взаимосвязей между объектами ограничивается психологическими возможностями людей. Поэтому при ранжировании большого числа объектов экспер­ты допускают существенные ошибки.

Парное сравнение

Парное сравнение представляет собой процедуру установления предпочтения объектов при сравнении всех возможных пар. В отличие от ранжирования, в котором осуществляется упорядочение всех объектов, парное сравнение объектов представляет собой значительно бо­лее простую задачу. При сравнении пары объектов возможны отношения либо порядка, либо порядка и экви­валентности, что доводится до сведения экспертов. В результате сравнения пары объектов О_i, О_j эксперт упорядочивает эту пару, высказывая, что либо О_i О_j , либо О_j  О_i , либо О_i  Оj. Выбор числового представления f естественно произвести так, что если О_i  О_j, то f(O_i) > f(O_j), если предпочтение в паре обратное, то знак неравенства заменяется на обратный, т.е. f(O_i) < f(O_j). Наконец, если объекты эквивалентны, то естественно полагать, что f(O_i) = f(O_j).

В практике экспертного оценивания используют следующие числовые представления:

1) Если О_i  О_j, то f(O_i) = 2,  f(O_j) = 0,

если О_i  О_j,     то

f(O_i) =   f(O_j) = 1;   (12.7)

2) если О_i  О_j, ,то f(O_i) = 1, f(O_j) = -1,

если О_i  О_j, то

f(O_i) = f(O_j) = 0.   (12.8)

Результаты сравнения экспертом всех пар удобно представить в виде таблицы, столбцы и строки которой составляют объекты, а в ячейках таблицы представляются числовые предпочтения. Таблица для числового представления (12.7) аналогична таблицам спортивных игр, например футбола, хоккея и т.п. В таблице 12.1 приведен пример отображения результатов парного сравнения 5 объектов при использовании представления (12.7). По диагонали таблицы проставлены единицы вследствие того,

что каждый объект эквивалентен самому себе.

Таблица 12.1 Пример отображения результатов парного сравнения пяти объектов

Oi	Oj
	O1	O2	O3	O4	O5
O1	1	2	2	1	2
O2	0	1	2	1	0
O3	0	0	1	0	1
O4	1	1	2	1	0
O5	0	2	1	2	1

Из табл. 12.1, например, следует, что объект О₁ пред­почтительнее объектов О₂, О₃, О₅ и эквивалентен объек­ту О₄. Объект О₂ предпочтительнее объекта О₃, эквива­лентен объекту О₄ и менее предпочтителен, чем объекты О₁, и О₅.

При групповом экспертном оценивании каждый экс­перт представляет результаты парного сравнения в виде таблицы.

Сравнение объектов во всех возможных парах не да­ет полного упорядочения объектов. Поэтому, естественно, возникает задача о ранжировке объектов на основе их парного сравнения. Решение этой задачи при определен­ных условиях возможно и рассматривается далее в подразделе 12.4.

Непосредственная оценка

Непосредственная оценка представляет собой проце­дуру приписывания объектам числовых значений в шка­ле интервалов. Эксперту предлагается поставить в соответствие каждому объекту точку на непрерывной числовой оси, например на отрезке [0,1]. Естественно потребовать, чтобы эквивалентным по сравниваемым показателям объектам приписывалось одно и то же число.

Измерение предпочтения объектов в шкале интерва­лов может быть осуществлено с достаточной степенью достоверности только в случае полной инфор­мированности экспертов о свойствах объектов. Эти усло­вия встречаются в экспертном оценивании не очень часто. С целью некоторого ослабления этих условий и, ко­нечно, за счет уменьшения точности измерения вместо непрерывной числовой оси используют балльную оценку, что эквивалентно квантованию числовой оси на отрезки, каждому из

которых приписывается определен­ный балл. Эксперт теперь определяет числовую оценку объекта – балл. Применяются 5-, 10- и 100-балльные шкалы.

Последовательное сравнение

Последовательное сравнение представляет собой ком­плексную процедуру измерения, включающую как ран­жирование, так и непосредственную оценку. При последовательном сравнении эксперт выполняет следующие операции:

1) осуществляет ранжирование объектов;

2) производит непосредственную оценку объектов на отрезке [0,1], полагая, что числовая оценка первого в ранжировке объекта равна единице:

f(Oi) = 1 ;

3) решает, будет ли первый объект превосходить по предпочтительности все остальные объекты, вместе взятые. Если да, то эксперт увеличивает значение числовой оценки первого объекта так, чтобы она стала  больше суммы числовых оценок остальных объектов, т.е.

.

В противном случае эксперт изменяет величину f(O₁) так, чтобы она стала меньше, чем сумма оценок остальных объектов;

4) решает, будет ли второй объект предпочтительнее, чем все последующие объекты, вместе взятые, и изменяет f(O₂) так же, как это описано для f(О₁) в пункте «3»;

5) продолжает операцию сравнения предпочтительности последующих объектов с остальными по ранжировке объектами и изменяет числовые оценки этих объектов в зависимости от своего решения о предпочтении.

Изложение процедуры выполнения последовательного сравнения объектов показывает, что система с отношениями должна содержать отношение порядка и операцию сложения свойств объектов. Такие системы с отношениями носят название экстенсивных систем. Для бесконечных экстенсивных систем доказано существование числовых представлений, единственных до преобразования подобия. Следовательно, измерение экстенсивных систем производится с использованием шкал отношений.

Рассмотренные четыре метода измерения: ранжирование, парное сравнение, непосредственная оценка и последовательное сравнение – обладают различными качествами, но приводят к близким результатам. Экспериментальная сравнительная оценка этих методов показала, что в ряде случаев наиболее эффективным является

комплексное применение всех методов для решения одной и той же задачи. При этом следует учитывать, что наиболее простым методом, требующим минимальных затрат, является ранжирование, а наиболее трудоемким для экспертов – метод последовательного сравнения. Метод парного сравнения без дополнительной обработки и ряда ограничений не дает полного упорядочения объектов.