Методы обработки экспертных решений

После проведения опроса группы экспертов осуществляется обработка результатов. Исходной информацией для обработки являются числовые данные,

выражающие предпочтения экспертов и содержательное обоснование этих предпочтений. Целью обработки является получение обобщенных данных и новой информации, содержащейся в скрытой форме в экспертных оценках. На основе результатов обработки формируется решение проблемы.

Наличие, как числовых данных, так и содержательных высказываний экспертов приводит к необходимости применения качественных и количественных методов обра­ботки результатов группового экспертного оценивания. Удельный вес этих методов существенно зависит от класса проблем, решаемых экспертным оцениванием.

Как уже отмечалось, все множество проблем можно разделить на два класса. К первому классу относятся проблемы, для решения которых имеется достаточный уровень знаний и опыта, т.е. имеется необходимый информационный потенциал. При решении проблем, относящихся к этому классу, эксперты рассматриваются как хорошие в среднем измерители. Под термином «хорошие в среднем» понимается возможность получения результатов измерения, близких к истинным. В случае получения результатов измерения, близких к истинным, суждения экспертов группируются вблизи истинного значения. Отсюда следует, что для обработки результатов группового экспертного оценивания проблем первого класса можно успешно применять методы математической статистики, основанные на осреднении данных.

Ко второму классу относятся проблемы, для решения которых еще не накоплен достаточный информационный потенциал. В связи с этим суждения экспертов могут очень сильно различаться друг от друга. Более того, суждение одного эксперта, сильно отличающееся от остальных мнений, может оказаться истинным. Очевидно, что применение методов осреднения результатов групповой экспертной оценки при решении проблем второго класса может привести к серьёзным ошибкам. Поэтому обработка результатов опроса экспертов в этом случае должна базироваться не на методах, использующих принципы осреднения, а на методах качественного анализа.

Учитывая, что проблемы первого класса являются наиболее распространенными в практике экспертного оценивания, основное внимание мы уделим методам обработки результатов экспертизы для этого класса проблем.

В зависимости от целей экспертного оценивания и выбранного метода измерения при обработке результатов опроса возникают следующие основные задачи:

· построения обобщенной оценки, объектов на основе индивидуальных оценок экспертов;

· построения обобщенной оценки на основе парного сравнения объектов каждым экспертом;

· определения относительных весов объектов;

· определения согласованного мнения экспертов;

· определение зависимостей между ранжировками;

· оценки надежности результатов обработки.

Задача построения обобщенной оценки объектов по индивидуальным оценкам экспертов возникает при групповом экспертном оценивании. Решение этой задачи зависит от использованного экспертами метода измерения.

При решении многих задач недостаточно осуществить упорядочение объектов по одному показателю или некоторой совокупности показателей. Желательно иметь численные значения для каждого объекта, определяющие относительную его важность по сравнению с другими объектами. Иными словами, для многих задач необходимо иметь оценки объектов, которые не только осуществляют их упорядочение, но и позволяют определять степень предпочтительности одного объекта перед другим. Для решения этой задачи можно применить метод непосредственной оценки. Однако эту же задачу при определенных условиях можно решить путем обработки оценок экспертов.

Определение согласованности мнений экспертов производится путем вычисления числовой меры, характеризующей степень близости индивидуальных мнений. Анализ значения меры согласованности способствует выработке правильного суждения об общем уровне знаний по решаемой проблеме и выявлению группировок мнений экспертов. Качественный анализ причин группировки мнений позволяет установить существование различных взглядов, концепций, выявить научные школы, определить характер профессиональной деятельности и т.п. Все эти факторы дают возможность более глубоко осмыслить результаты опроса экспертов.

Обработкой результатов экспертного оценивания можно определять зависимости между ранжировками различных экспертов и, тем саамы, устанавливать единство, и различие в мнениях экспертов. Важно установить зависимость между ранжировками, построенными по различным показателям сравнения объектов. Выявление таких зависимостей позволяет вскрыть связанные показатели сравнения и, может быть, осуществить их группировку по степени связи. Важность задачи определения зависимостей для практики очевидна. Например, если показателями сравнения являются различные цели, а объектами – средства достижения целей, то установление взаимосвязи между ранжировками, упорядочивающими средства с точки зрения дости­жения целей, позволяет обоснованно ответить на вопрос, в какой степени достижение

одной цели при данных средствах способствует достижению других целей.

Оценки, получаемые на основе обработки, представляют собой случайные объекты, поэтому одной из важных задач процедуры обработки является определение их надежности. Решению этой задачи должно уделяться соответствующее внимание.

Обработка результатов экспертизы представляет собой трудоемкий процесс. Выполнение операций вычисления оценок и показателей их надежности вручную связано с большими трудовыми затратами даже в случае решения простых задач упорядочения. В связи с этим целесообразно использовать вычислительную технику. Применение ЭВМ выдвигает проблему разработки машинных программ, реализующих алгоритмы обработки результатов экспертного оценивания.

Групповая оценка объектов

Рассмотрим алгоритмы обра­ботки результатов экспертного оценивания множества объектов. Пусть m экспертов произвели оценку n объек­тов по l показателям. Результаты оценки представлены в виде величин , где j – номер эксперта, i – номер объекта, h – номер показателя (признака) сравнения. Если оценка объектов произведена методом ранжирова­ния, то величины  представляют собой ранги. Если оценка объектов выполнена методом непосредственной оценки или методом последовательного сравнения, то величины  представляют собой числа из некоторого отрезка числовой оси, или баллы. Обработка результа­тов оценки существенно зависит от рассмотренных мето­дов измерения.

Рассмотрим вначале случай, когда величины

 (i = 1, …, n; j = 1, 2, …, m; h = 1, 2, …, l)

получены мето­дами непосредственной оценки или последовательного сравнения, т.е.  являются числами, или баллами. Для получения групповой оценки объектов в этом случае можно воспользоваться средним значением оценки для каждого объекта:

   (i = 1, 2,…, n),   (12.12)

где q_hj  – коэффициенты весов показателей сравнения объектов, k_j – коэффициенты компетентности экспертов.

Коэффициенты весов показателей и компетентности объектов являются нормативными величинами:

;          (12.13)

Коэффициенты весов показателей могут быть опреде­лены экспертным путем. Если q_hj – коэффициент веса h-го показателя, даваемый j-м экспертом, то средний ко­эффициент веса h-го показателя по всем экспертам ра­вен:

      (h = 1, 2, …, l).   (12.14)

Коэффициенты компетентности экспертов можно вы­числить по апостериорным данным, т.е. по результатам оценки объектов. Основной идеей этого вычисления яв­ляется предположение о том, что компетентность экспер­тов должна оцениваться по степени согласованности их оценок с групповой оценкой объектов.

Способ сумм рангов

Способ сумм рангов заключается в ранжировании объектов по величинам сумм рангов, полученных каждым объектом от всех экспертов. Для матрицы ранжировок ||r_ij|| составляются суммы:

  (i = 1, 2, …, n).   (12.15)

Далее объекты упорядочиваются по цепочке неравенств:

r₁  <   r₂   < …< r_n.

Например, результаты ранжировки пяти объектов пятью экспертами представлены в таблице 12.2.

Таблица 12.2 Результаты ранжировки пяти объектов пятью экспертами

Эi	Oj
	O1	O2	O3	O4	O5
Э1	2	1	3	4	5
Э2	2	1	3	5	4
Э3	3	1	2	4	5
Э4	2	3	1	4	5
Э5	1	2	4	3	5
	10	8	13	20	24

Результаты вычисления сумм рангов для всех объектов приве­дены в последней строке таблицы 12.2. Из сравнения сумм рангов полу­чаем цепочку неравенств:

r₂  <   r₁   < r₃  <   r₄ <   r₅.

Отсюда следует обобщенная ранжировка:

O₂   O₁  O₃    O₄  O₅.   (12.16)

В данном примере рассмотрен случай, когда отношение между объектами является отношением строгого порядка. Если имеется и отношение эквивалентности, то процедура построения обоб­щенной ранжировки по сумме рангов не изменяется.

Для учета компетентности экспертов достаточно умножить каждую i-ю ранжировку на коэффициент ком­петентности j-го эксперта:

0  k_j  1.

В этом случае вы­числение суммы рангов для i-гo объекта производится по следующей формуле:

  (i = 1, 2, …, n).   (12.17)

Обобщенная ранжировка с учетом компетентности экс­пертов строится на основе упорядочения сумм рангов для всех объектов.

Следует отметить, что построение обобщенной ранжировки по суммам рангов является корректной процедурой, если ранги назначаются как места объектов в виде натуральных чисел 1, 2, …, n. Если назначать ранги произвольным образом, как числа в шкале порядка, то сумма рангов, вообще говоря, не сохраняет условие монотонности преобразования и, следовательно, можно получать различные обобщенные ранжировки при различных отображениях объектов на числовую систему. Нумерация мест объектов может быть произведена единственным образом с помощью натуральных чисел.

Обработка парных сравнений объектов

При решении задачи оценки большого числа объектов (при ранжировании, определении относительных весов, балльной оценке) возникают трудности психологического характера, обусловленные восприятием экспертами множества свойств объектов. Эксперты сравнительно легко решают задачу парного сравнения объектов. Возникает вопрос, каким образом получить оценку всей совокупности объектов на основе результатов парного сравнения, не накладывая условия транзитивности? Рассмотрим алгоритм решения этой задачи. Пусть т экспертов производят оценку всех пар объектов, давая числовую оценку:

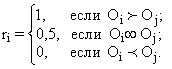   (12.18)

Если при оценке пары О_i, О_j в пользу предпочтения  О_i   О_j высказались m_i экспертов, в пользу предпочтения О_j   О_i высказались m_j экспертов и m_h экспертов считают эти объекты равноценными, то оценка математического ожидания случайной величины (r_ij) равна:

.   (12.19)

Общее количество экспертов равно:

m = m_i  +  m_h  +   m_j.

Определяя отсюда m_h  и подставляя его в формулу (12.19), получим:

      (i, j = 1, 2, …, n).   (12.20)

Очевидно, что

x_ij + x_ji = 1.

Совокупность величин x_ij образует матрицу n × m, на основе которой можно по­строить ранжировку всех объектов и определить коэф­фициенты относительной важности объектов.

Коэффициенты относительной важности позволяют определить, во сколько раз один объект превосходит другой объект по сравниваемым показателям. Коэффициент важности может быть вычислен по формуле:

.   (12.21)