1) Определение ряда:
.
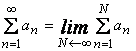2) Необходимый признак сходимости ряда: если ряд 
сходится, то
.
3) Геометрическая прогрессия
.
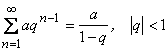Сумма членов бесконечно убывающей прогрессии представляет сходящийся числовой ряд.
4) Гармонический ряд
(расходится).
5) Признак Даламбера: если существует 
, то
а) если D < 1, то ряд сходится;
б) если D > 1, то ряд расходится.
6) Признак Коши: если существует 
то при K < 1 ряд сходится, при K > 1 — расходится.
7) Абсолютная сходимость:
Если ряд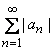 
сходится, то ряд 
сходится абсолютно.
8) Признак Лейбница: если 
и 
при 
, то знакочередующийся ряд
сходится.
9) Радиус сходимости степенного ряда
определяется по формуле 
, если предел существует.
10) Ряд Маклорена:
11) Разложение функций в степенные ряды:
а) 
;
б) 
;
в) 
;
г) 
;
е) 
;
ж) 
.
12) Ряд Тейлора:
.
13) Ряды в комплексной области:
.
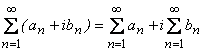14) Абсолютная сходимость рядов с комплексными членами.
Если ряд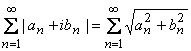 
сходится, то ряд 
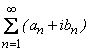сходится абсолютно.
15) Формула Эйлера 
.
16) Тригонометрический ряд Фурье кусочно-гладкой функции f(x) периода T=2l:
,
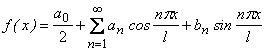где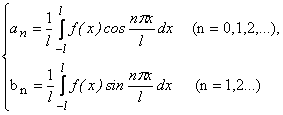 
— коэффициенты Фурье функции f(x).
В точках разрыва функции f(x) сумма ряда:
.
17) Если 2l — периодическая функция четная, то
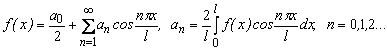
если f(x) — нечетная, то
.
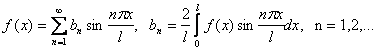Пример 66: Исследовать ряд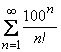 
на сходимость.
Решение: Согласно признаку Даламбера, получим:
,
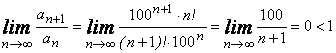следовательно, ряд сходится 
.
Пример 67: Исследовать ряд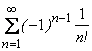 
на сходимость.
Решение: Это ряд типа Лейбница и 
при 
, и члены по абсолютной величине убывают, следовательно, ряд сходится.
Пример 68: Установить радиус сходимости ряда 
.
Решение: используем формулу для определения радиуса сходимости
R=
,
следовательно, ряд сходится в интервале (-1; 1). Чтобы ответить на вопрос, будет ли сходиться ряд при х = -1 и х = 1, то в каждом случае исследуется на сходимость ряд при х = -1 и х = 1:
— расходится (это гармонический ряд);
— сходится условно.
Таким образом, промежуток сходимости 
.
Пример 69: Применяя ряды, вычислить 
.
Решение: Соответствующий неопределенный интеграл не выражается в элементарных функциях и применить формулу Ньютона-Лейбница нельзя; но, применяя степенные ряды, этот интеграл можно вычислить приближенно. Разделим почленно ряд для sin x на х, получим:
Интегрируя почленно, получим:
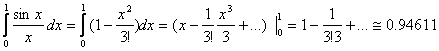
Ряд знакочередующийся, по признаку Лейбница он сходится. Ограничившись тремя членами, допустим погрешность меньше 
.
Пример 70: Разложить в ряд по степеням х функцию 
.
Решение: известно, что имеет место разложение:
.
где вместо –х подставлен х. В этом новом разложении вместо х запишем –х2:
Полученный ряд сходится при |x|<1.
Пример 71: Разложить функцию f (x) = 2x при 
в ряд Фурье.
Решение: при разложении функции в ряд Фурье необходимо построить график этой функции на промежутке 
и периодически его продолжить на всю числовую ось (рис. 12.1).
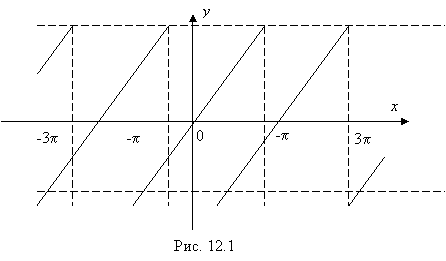
Условия разложимости функции в ряд Фурье выполнены. В точках разрыва ряд Фурье сходится к числу 
, то есть сумма ряда Фурье в точках разрыва равно нулю. Найдем коэффициенты Фурье (
, так как функция нечетная):
.
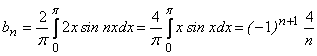Следовательно, 
.