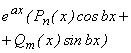1)  Дифференциальное уравнение с разделяющимися переменными

имеет общий интеграл

.

Особые решения, не входящие в общий интеграл, определяются из уравнений N₁(x) = 0  и     M₂(y) = 0.

2)  Однородное дифференциальное уравнение первого порядка

P(x,y) dx + Q (x,y) dy = 0,

где P(x,y) и Q(x,y)  — однородные непрерывные функции одинаковой степени, решается с помощью подстановки y = uv, где u = u(x) — новая функция.

3)  Линейное дифференциальное уравнение первого порядка

A(x)y^‘ + B(x)y + C(x) = 0

можно решить с помощью подстановки y = uv, где u = u(x), v = v(x) (метод Эйлера-Бернулли).

4)  Понижение порядка дифференциального уравнения второго порядка:

а) если y² = f(x), то общее решение

;

б) если y² = f(y),  то общий интеграл

;

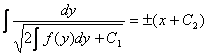в) если y² = f(y¢),  то общий интеграл уравнения можно найти из соотношения

,       где y¢ = p;

г) если y² =f(x,y¢ ), то, полагая y¢ = p, приходим к уравнению первого порядка:

.

д) если , то, полагая y^‘=p, придем к уравнению

.

5)  Общее решение линейного однородного дифференциального уравнения второго порядка

имеет вид

где       y₁ и y₂  — линейно независимые частные решения .

,

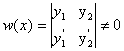где       w(x) – определитель Вронского.

6) Общее решение линейного неоднородного дифференциального уравнения второго порядка

имеет вид

,

где y_r — частное решение данного неоднородного уравнения.

7)  Общий вид решений уравнения  (p, q — постоянные) в зависимости от корней характеристического уравнения k² + pk + q = 0.

                                                                           Таблица 13.1

Характер корней `	Вид общего решения
Корни  —  действительные
Корни
Корни комплексные

8)  Характер частного решения y₂ неоднородного уравнения  (p, q — постоянные) в зависимости от правой части f(x).

Таблица 13.2

Правая часть f(x)	Случаи корней характеристического уравнения	Вид частного решения yr
1	2	3
— многочлен степени n	0 — корень уравнения	— многочлен с неопределенными коэффициентами
	0 — корень характеристического уравнения
	а — не является корнем характеристического уравнения
	а — является корнем характеристического уравнения кратности 2
	Числа  — не корни характеристического уравнения
	Числа  — корни  характеристического уравнения

Продолжение табл. 13.2

1	2	3
	— не корни характеристического уравнения
	- корни характеристического уравнения
Примечание.  — многочлены, в которые введены неопределенные коэффициенты соответственно степеней .

Пример 72:  Найти частное решение уравнения

.

Решение:  Это уравнение с разделяющимися переменными.

Разделяя переменные, получаем

.

Интегрируя, находим общий интеграл:

.

Подставляя в общий интеграл , будем иметь

.

Подставляя С в общий интеграл, найдем частное решение:

.

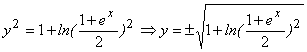Начальное условие y(0) = 1 говорит о том, что частное решение будет

.

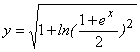9)  Метод вариации: частное решение неоднородного уравнения ищут в виде

,

для чего решают систему                 

Пример 73:  Решить уравнение .

Решение:  Имеем уравнение с разделяющимися переменными

.

Интегрируя, найдем

.

Потенцируя, получим

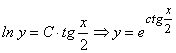  — общее решение уравнения.

Пример 74:  Проинтегрировать уравнение

.

Решение:  Деля на  обе части уравнения, получим уравнение с разделенными переменными:

.

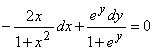Интегрируя, получим:

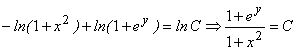  — общий интеграл.

Пример 75. Решить уравнение .

Решение:  Запишем уравнение в виде

,

получим однородное уравнение относительно x и y.

Даем подстановку , или , тогда . Подставив y, y¢  в исходное уравнение, получаем:                                                                  .

Это уравнение с разделяющимися переменными, то есть

.

Интегрируя, находим

Так как , введя обозначение , получим

,

где       ,    .

Заменим u на , получим общий интеграл

  — общее решение.

Замечание. При разделении переменных мы делили обе части уравнения на  и могли потерять решения, которые обращают в нуль это произведение.

Положим х=0 и , но  в силу подстановки , а из  следует, что .

Проверкой убеждаемся, что y = -x и y = x являются решениями исходного уравнения.

Пример 76:  Решить линейное уравнение

.

Решение:  Полагаем , тогда , подставив в данное уравнение, получим

Таким образом, общее решение будет:

.

Пример 77: Найти общее решение уравнения .

Решение:  Интегрируя последовательно два раза эти уравнения, получаем

 — общее решение.

Пример 78:  Решить уравнение .

Решение:  Данное уравнение не содержит явно у. Полагаем , тогда , получим при подстановке:

.

Учитывая, что , будем иметь:

 — общее решение.

Пример 79:  Решить уравнение .

Решение: Уравнение явно не содержит х. Даем подстановку   

 получаем     ,

тогда 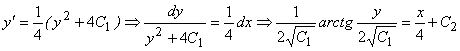 — общий интеграл исходного уравнения.

Пример 80: Решить линейное уравнение .

Решение:  Составим характеристическое уравнение

.

Согласно структуре, общее решение будет:

.

Пример 81:  Решить уравнение .

Решение:  Характеристическое уравнение  имеет равные корни , следовательно,

 — общее решение.

Пример 82:  Решить уравнение               .

Решение:  Корни уравнения  — мнимые: , следовательно, согласно структуре, общее решение будет:

.

Пример 83: Решить уравнение .

Решение: сначала решим соответствующее однородное уравнение . Корни характеристического уравнения   приводят к общему решению . Далее найдем частное решение неоднородного уравнения, методом неопределенных коэффициентов. Так как число нуль не входит в состав корней характеристического уравнения (см. табл. 13.1, случай ), то вид его будет:

.

Подставляя у и  в исходное уравнение, найдем:

2A — 3Ax — 3B = x + 1, .

Тогда  — частное общее решение неоднородного уравнения. Следовательно, общее решение неоднородного уравнения:

.

Пример 84:  Записать вид частного решения неоднородного уравнения:

.

Решение:  Сначала найдем общее решение соответствующего однородного уравнения . Корни уравнения  — комплексные , поэтому общее решение однородного уравнения будет:

.

Так как числа  являются однократными корнями характеристического уравнения, то частное решение данного неоднородного уравнения ищут в виде:

.

Пример 85:  Решить уравнение .

Решение:  Сначала решим соответствующее однородное уравнение .

Корни уравнения  — чисто мнимые, поэтому .

Число  является однократным корнем характеристического уравнения, следовательно, вид частного решения неоднородного уравнения будет:

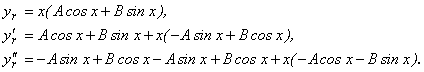
Подставляя в исходное уравнение и сравнивая коэффициенты, получим:

Частное решение будет

.

Следовательно, общее решение исходного уравнения будет:

.

Пример 86:  Решить уравнение  методом вариации произвольных постоянных.

Решение:  Решение будем искать по такому алгоритму:

а) найти линейно независимые частные решения y₁ и y₂, для чего решим характеристическое уравнение , получим ;

б) составим систему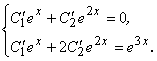                      

из которой найдем   и :         

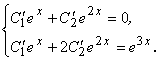
Система имеет единственное решение, так как ее главный определитель совпадает с определителем Вронского  и по правилу Крамера находим:

,               , то есть

,           ;

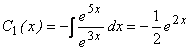в) находим частное решение исходного неоднородного уравнения в виде:

, то есть ;

г) запишем искомое решение: .