1) Криволинейный интеграл первого рода (по длине дуги) от функции  — непрерывной, взятый по кусочно-гладкой кривой  равен

.

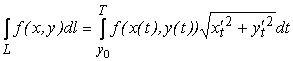Если кривая задана уравнением , то

.

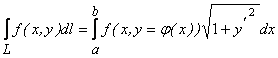Аналогично дается определение криволинейного интеграла для случая пространственной кривой.

2)  Криволинейный интеграл второго рода (по координатам):

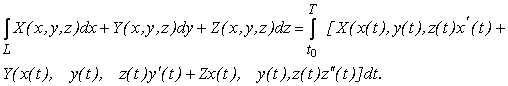
Если L задана уравнением , то:

.

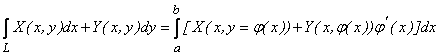3)  Если имеет место условие

,

то криволинейный интеграл не зависит от формы пути L  и

,

где  и  — начальная и конечная точки кривой L соответственно.