Рассмотрим два случая нагружения ремня (рис. 15.5):  и .

По условию равновесия шкива имеем:

или

.   (15.17)

Геометрическая длина ремня не зависит от нагрузки и остается неизменной как в ненагруженной, так и в нагруженной передаче. Следовательно, дополнительная вытяжка ведущей ветви компенсируется равным сокращением ведомой ветви. В соответствии с этим имеем:

;    

или

,           (15.18)

где  – начальное натяжение ремня;  – изменение натяжений ведущей и ведомой ветвей ремня.

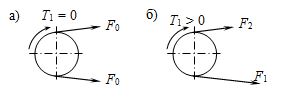
Рис. 15.5. Нагружение ремня

Из равенств (15.17) и (15.18) следует:

;     .  (15.19)

Уравнения (15.19) устанавливают изменение натяжений ведущей и ведомой ветвей ремня в зависимости от нагрузки , но не вскрывают тяговой способности передачи, связанной со значением силы трения между ремнем и шкивом. Такая связь установлена Эйлером:

;    ;    , (15.20)

где  – коэффициент трения;  – угол скольжения (см. рис. 15.4);  – в данном случае рабочее начальное натяжение ремня.

По формулам (15.20) можно определить минимально необходимое начальное натяжение ремня , при котором еще возможна передача заданной нагрузки ().

Если предельное начальное натяжение ремня

,

то начинается буксование ремня.

Из формул (15.20) следует, что увеличение значений  и  благоприятно сказывается на работе передачи. Эти выводы приняты за основу при создании конструкций клиноременной передачи (использован принцип искусственного

повышения трения за счет заклинивания ремня в канавках шкива) и передачи с натяжным роликом (увеличивается угол обхвата ).

При круговом движении ремня со скоростью  возникает дополнительное натяжение ремня () от центробежных сил:

,

где  – плотность материала ремня, кг/м³; А – площадь поперечного сечения ремня, м².

Натяжение  ослабляет полезное действие предварительного натяжения : уменьшает силу трения и, соответственно, уменьшает тяговую способность передачи. Влияние центробежных сил на работоспособность передачи существенно при скоростях  м/с.