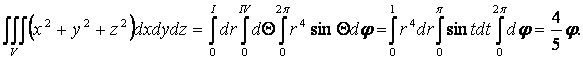1) Поверхностные интегралы первого рода (по площади поверхности).
Определение. Поверхностным интегралом первого рода от функции f(x,y,z) – непрерывной на поверхности Q, называется число
.
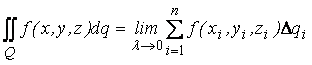2) Если поверхность задана уравнением z=z(x,y), то
.
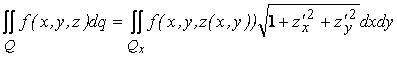3) Поверхностным интегралом второго рода (по координатам) называется число
где 
— проекция элемента площади поверхности на плоскость ХОУ.
Аналогичным образом определяются интегралы
.
4) Обобщенный поверхностный интеграл по координатам:
,
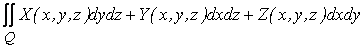где 
— функции от x,y,z — непрерывные на поверхности Q.
Замечание: С гидроаэродинамической точки зрения поверхностный интеграл по координатам дает поток вектора
через поверхность Q в выбранном направлении нормали к поверхности.
5) Формула Стокса:
,
где Q – кусочно-гладкая поверхность, L – замкнутый контур, ограничивающий конечную кусочно-гладкую двустороннюю поверхность Q, X,Y,Z — функции непрерывные вместе со своими частными производными первого порядка.
6) Формула Остроградского:
где Q – замкнутая поверхность, ограничивающая объем V.
Замечания:
а) выражение 
, где 
и называется дивергенцией вектора 
;
б) поток вектора через замкнутую поверхность Q можно вычислить по формуле Остроградского:
;
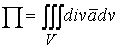в) величина интеграла 
и называется циркуляцией вектора 
вдоль замкнутого контура L (может быть вычислена по формуле Стокса).
Пример 87: Вычислить 
по одному витку винтовой линии:
.
Решение: Используя параметрическое задание линии, получим
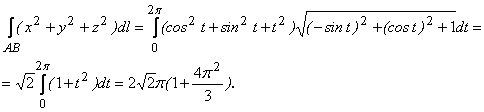
Пример 88: Вычислить интеграл 
, где АВ – часть логарифмической кривой 
.
Решение: Так как кривая задана уравнением 
, то 
, поэтому
Пример 89: Вычислить интеграл 
вдоль отрезка АВ, соединяющего точки A(1;2;-1) и B(3;3;4).
Решение: составим уравнения пути интегрирования, для чего составим уравнение прямой в пространстве, проходящей через две заданные точки:
.
В параметрической форме эти уравнения будут:
.
Тогда
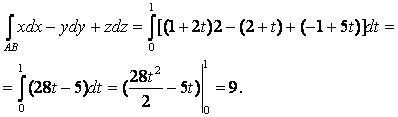
Пример 90: Вычислить 
по дуге АВ параболы 
.
Решение: Примем х за параметр, получим:
Пример 91: Вычислить интеграл 
, если область D ограничена линиями 
.
Решение: выберем определенный порядок интегрирования – внешнее по х, внутреннне по у (рис. 16.1)
Пример 92: Переходя к полярным координатам, вычислить двойной интеграл
,
где D – первая четверть круга радиуса R = 4 с центром в начале координат.
Решение: Так как 
, то
.
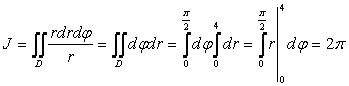Пример 93: Вычислить тройной интеграл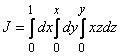 
.
Решение: Вычисление начнем из внутреннего интеграла:
.
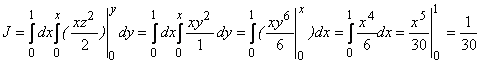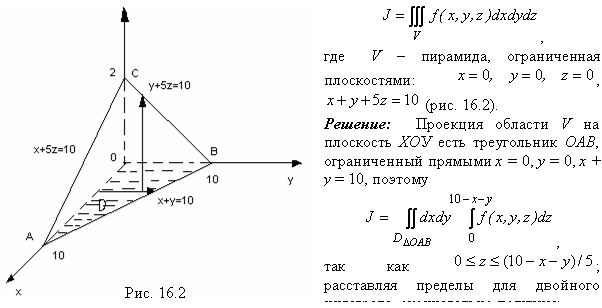
Пример 94: Расставить пределы интегрирования в тройном интеграле
.
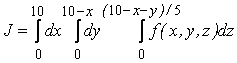Пример 95: Найти площадь части конической поверхности 
, вырезаемой плоскостями x = 0, y = 0, x + y = 1, x + y = 2 и лежащей в первой октанте.
Решение: Для нахождения площади поверхности используем поверхностный интеграл первого рода, для чего найдем:
.
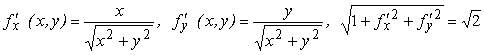Следовательно,
.
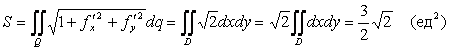Пример 96: Вычислить поверхностный интеграл 
по верхней стороне полусферы 
.
Решение: Данную поверхность можно задать уравнением 
, поэтому
,
где D - круг 
плоскости ХОУ, на которую проектируется поверхность Q (полусфера).
Вычисляя двойной интеграл, получим:
.
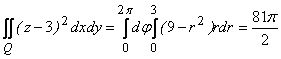Пример 97: Используя формулу Остроградского, вычислить поверхностный интеграл 
по внешней стороне замкнутой поверхности пирамиды (рис. 10).
Решение: Используя формулу Остроградского, найдем 
.
Так как 
, то
и 
.
Следовательно,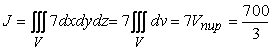 
,
где Vпир — объем пирамиды ОАВС.
Пример 98: Вычислить тройной интеграл 
, если область V – шар 
.
Решение: Используем сферические координаты:
x = r sin Q cos j, y = r sin Q sin j, z = r cos Q (*)
В области V1, являющейся образом в области V при указанном преобразовании (*), переменные r, j, Q меняются в следующих пределах: 0 £ R £ 1, 0 £ j £ 2p, 0 £ Q £ p. Так как подынтегральная функция 
, а Якобиан равен r2 sin Q, то по формуле
