Результат действия над действительными числами всегда существует и однозначен для сложения, вычитания, умножения, возведения в натуральную степень, деления (за исключением деления на нуль). Что касается извлечения корня, то во множестве вещественных чисел оно не всегда выполнимо. Извлечение корня четной степени из отрицательного числа приводит к понятию комплексного числа. Так, выражения , … не имеют смысла в области вещественных чисел, поэтому уравнения х²+ 4 = 0, х²-2х + 5= 0 неразрешимы во множестве действительных чисел. Следовательно, множество действительных чисел расширяют до множества комплексных чисел присоединением к действительным мнимых чисел для того, чтобы извлечение корня сделать выполнимым, а алгебраические уравнения – разрешимыми.

Число  = i называют мнимой единицей, т.е. по определению принимают i² =-1.

Определение.  Выражение z = x – iy, где х, у Î R, а  i - мнимая  единица, называют комплексным числом. Число х называется действительной частью, а у — мнимой частью комплексного числа x + iy.

Равенство чисел: x + iy = а +ib,  если х = а, у = b.

Сопряженные числа: x + iy и x – iy.

Имеют место действия над комплексными числами:

1)         (a + ib) + (c + id) = (a + c) + i(b + d);

2)         (a + ib) — (c + id) = (a — c) + i(b — d);

3)         (a + ib)×(c + id) = (ac — bd) + (ad + bc)I;

4)         (a + ib) / (c + id) = (ac + bd) / (c² + d²) + (bc – ad ) / (c² + d²),  (c + id ≠ 0).

Отметим, что во множестве комплексных чисел нет отношения «больше» или «меньше», т.е. это множество не упорядочено и свойства неравенств для комплексных чисел не имеют места.

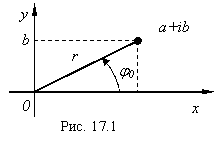Комплексные числа геометрически изображаются на комплексной плоскости хоу, где х, у – декартовы координаты точки М(a, b) (рис. 17.1).

Длина вектора  называется модулем комплексного числа и обозначается :

.

Угол  j  между положительным направлением оси абсцисс и вектором  называется аргументом комплексного числа  a + ib.

Так как этот угол определяется с точностью до 2pn, n Î Z, то, обозначив наименьший по абсолютной величине угол между осью ох и  через j₀, получим:

j = j₀+ 2pn,  (n = 0, ±1, …).

Этот угол называют главным значением аргумента комплексного числа  a + ib,  находится в интервале  -p < j₀ £  p.

Отметим, что существуют разные формы записи комплексного числа. Форм записи употребляют три: алгебраическую, тригонометрическую, показательную.

Записи:                 a + ib – алгебраическая;

                     z = a + ib = r(cos j + I sin j) —  тригонометрическая;

                     z = re^ij —  показательная (использовали формулу Эйлера).

Модели, выражающие действия в тригонометрической и показательной формах:

;

;

.

При r = 1:  — называется формулой Муавра.

 k = 0, 1, 2, …, n-1.

Пример 99:  Найти модули и главные значения аргументов комплексных чисел: а) 2 + 2i;            б) -2 + 2i;        в) .

Решение: 

а) (желательно сделать схематические рисунки) по определению модуля комплексного числа    ;       ;

б) ;                 ;

в) ;         .

Пример 100: Записать тригонометрическую и показательную формы для приведенных в примере 99 чисел.

Решение:  а) ;

б) ;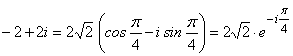

в) .

Пример 101:  Умножить и разделить комплексные числа:  а) 2 + 2i;    б) -2 + 2i;

Решение:  Используем результаты примера 100:

, тогда по моделям умножения и деления будем иметь:

;

.

Пример 102:  Вычислить .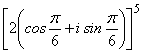

Решение:  Применяя действие возведения в степень, получим:

.

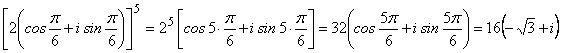Пример 103:  Вычислить .

Решение:  Найдем модель и главное значение числа -1:  , тогда

, k = 0, 1, 2;

;

.