Определение. Пусть А и В – две формулы, зависящие от одного и того же списка переменных. Будем называть их равносильными, если для любого набора значений переменных  они принимают одинаковые значения.

Рассмотрим основные равносильности логики высказываний.

Пусть А, В, С – произвольные формулы. Тогда справедливы следующие свойства логических операций (табл. 2.9):

Таблица 2.9 Свойства логических операций

Любая из этих равносильностей легко может быть доказана с помощью таблицы истинности.

Пример 23.

Рассмотрим одно из правил поглощения А  (А  В) = А.

Таблица 2.10 Доказательство правила поглощения

По табл. 12 видно, что результирующий столбец и столбец А совпадают на все наборах. Значит, формулы действительно равносильны.

Однако часто равносильность экономнее доказывать без составления полной таблицы истинности, а с помощью приведенных выше равносильностей.

Пример 24.

1) Доказать равносильность формулы, используя логические законы: .

2) Упростить формулу: .

3) Определить, является ли формула тавтологией, противоречием или ни тем, ни другим:

· ;

· ;

· ;

· ;

· .

Решение.

1) .

2)

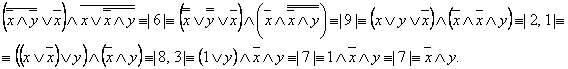
3) a)

Поскольку формула при любых значениях переменных равна нулю, то данная формула является противоречием.

б) .

Исходная формула не является ни тавтологией, ни противоречием, поскольку её значение зависит от значений переменных.

в)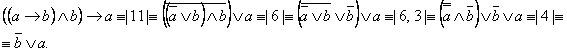

Исходная формула не является ни тавтологией, ни противоречием, поскольку её значение зависит от значений переменных.

г)

Исходная формула не является ни тавтологией, ни противоречием, поскольку её значение зависит от значений переменных.

д)

Поскольку формула при любых значениях переменных равна единице, то данная формула является тавтологией.