Аннуитетом называется серия платежей, произведённая в фиксированные интервалы времени за определённое число периодов. Например, выплаты по 300 долл. США в конце каждого из 5 лет будут называться пятилетним аннуитетом.
Платежи могут быть:
· регулярными и нерегулярными;
· положительными (поступления), отрицательными (выплаты) и смешанными;
· верными, т.е. подлежащими немедленной уплате, и условными, т.е. выплачиваемыми при наступлении какого-либо события;
· постоянными (с одинаковыми платежами) и переменными.
Поток платежей, все члены которого – положительные величины, а временные интервалы между платежами одинаковы, называют финансовой рентой. К примеру, финансовой рентой является получение процентов по облигации с фиксированной ставкой доходности, процентов по депозиту с начислением простых процентов и др.
Рента включает в себя следующие характеристики:
· член ренты – размер отдельного платежа;
· размер ренты – размер отдельного платежа;
· срок ренты – время от начала первого периода ренты до конца последнего периода;
· процентную ставку.
Платежи могут осуществляться как в начале периода (рента пренумерандо), так и в конце периода (рента постнумерандо).
Расчёты по аннуитетам обычно предусматривают определение одного из двух показателей: современной или наращенной стоимости ренты. Наращенная стоимость ренты – сумма наращенных стоимостей всех платежей по ренте. Аналогично современная стоимость ренты – сумма современных стоимостей всех членов ренты.
Графическую интерпретацию расчета наращенной стоимости ренты (рис. 2.3) рассмотрим на примере 1.
Пример 1
Пусть имеется 10 000 долларовая 5-летняя облигация внутреннего валютного займа с фиксированным платежом в конце каждого года 300 долл. США. Пусть на рынке действует ставка доходности 10 % годовых.
Решение:
Наращенная стоимость платежа составит:
· производимого в конце первого года:
300 (1 + 0,1)4 = 439,23 долл.;
· второго платежа
300 (1 + 0,1)3 = 399,3 долл.
и т.д.
Сумма наращенных стоимостей всех платежей (SA) составит:
SA = 300 (1 + 0,1)4 + 300 (1 + 0,1)3 + 300 (1 + 0,1)2 + 300 (1 + 0,1)1 + 300 (1 + 0,1)0 =
= 300 [(1,1)4 + (1,1)3 + (1,1)2 + (1,1)1 + (1,1)°] = 1831,53 долл.
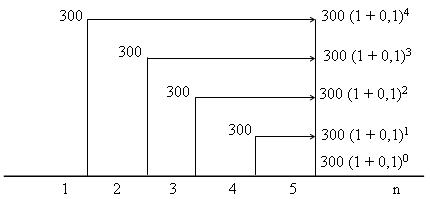
Рис. 2.3. Процедура расчета наращенной суммы пятилетней ренты постнумерандо
В общем случае задача расчета наращенной стоимости аннуитета будет иметь следующий вид. Пусть имеется ряд платежей (Rt), выплачиваемых через время nt от начального момента времени действия ренты n0, общий срок выплат n лет, проценты начисляются 1 раз в году по ставке сложных процентов (i). Тогда, по определению ренты, наращенная стоимость аннуитета составит:
![]() . (2.1)
. (2.1)
Для ренты с постоянными выплатами постнумерандо с началом выплат в конце первого года можно упростить процедуру расчёта. Из формулы (2.1) следует:
![]() .
.
Это уравнение представляет собой сумму членов геометрической прогрессии, определяемой как
![]() . (2.2)
. (2.2)
Понятно, что для ренты с платежами в начале периода, т.е. ренты пренумерандо, число периодов начисления процентов увеличивается на 1. Так, расчет sA для условий рассматриваемого примера ренты пренумерандо будет выглядеть:
sA = 300 (1 + 0,1)5 + 300(1 + 0,1)4 + 300(1 + 0,1)3 + 300(1 + 0,1)2 + 300(1 + 0,1)1 = 2 014,68.
В общем виде формула расчета sA для ренты пренумерандо будет выглядеть:
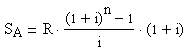 . (2.3)
. (2.3)
Процедуру расчета повременной (дисконтированной) стоимости (РA) можно представить аналогичным образом. Для условий примера ренты постнумерандо расчёт современной стоимости ренты показан на рис. 2.4.
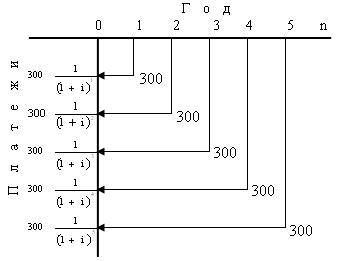
Рис. 2.4 Процедура расчета современной стоимости ренты постнумерандо
Современная стоимость первого платежа, производимого в конце первого года, составит ![]() , второго – соответственно
, второго – соответственно ![]() и т.д. Тогда сумма современной стоимости всех платежей ренты будет:
и т.д. Тогда сумма современной стоимости всех платежей ренты будет:
![]() .
.
В общем виде для условий ренты постнумерандо формулу расчета современной стоимости можно записать:
![]() . (2.4)
. (2.4)
Если платежи по ренте постоянные, а выплаты регулярно начисляются в конце первого года, формула (2.4) будет иметь вид:
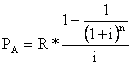 . (2.5)
. (2.5)
Для ренты пренумерандо выражение (2.5) преобразуется следующим образом:
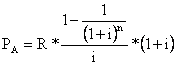 .
.
Формулы 2.1 – 2.5 можно применять с корректировкой, учитывая разнообразие условий ренты, начисление процента несколько раз в году, несинхронность начисления процента и выплаты платежа и иных обстоятельств. Более того, вторичные задачи по аннуитетам (определение сроков ренты, фактической процентной ставки) также могут быть поставлены и решены. Знание аннуитета, безусловно, расширяет возможности финансового анализа. Проиллюстрируем их одним лишь примером.
Пример 2
Предположим, некая фирма берет кредит в размере 100 тыс. р. на 3 года с условием равных выплат долга в течение этих трех лет. Кредитор должен получить проценты
за кредит в конце каждого года из расчета 6 % годовых. Необходимо определить сумму ежегодного платежа кредитору.
Решение:
Следует иметь в виду, что ежегодно заемщик платит начисленные проценты с суммы долга и часть долга (ссуда погашается в течение кредитного периода).
Очевидно 100 тыс. р. – современная (дисконтированная) стоимость всех трех платежей (R). Необходимо учесть, что это платежи равные.
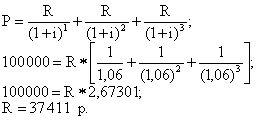
Схема погашения ссуды показана в таблице 2.2.
Таблица 2.2 Схема погашения кредита и процентов по нему
|
Год |
Задолженность кредитору на начало года |
Платежи |
Задолженность кредитору на конец года |
||
|
всего |
в том числе |
||||
|
процент |
ссуда |
||||
|
01 |
100 000 |
37 411 |
6 000 |
31 411 |
68 589 |
|
02 |
68 589 |
37 411 |
4 115 |
33 296 |
35 293 |
|
03 |
35 293 |
37 411 |
2 118 |
35 293 |
– |
|
Итого |
– |
112 233 |
12 233 |
100 000 |
– |
Обратите внимание, что в структуре ежегодного платежа доля процента снижается. Абсолютные размеры процента по данным таблицы 2.2 составляют 6 000, 4 115, 2 118. В то же время доля погашаемой ссуды растет.