Опишем сначала алгоритмы, известные как цифровые дифференциальные анализаторы (сокращенно ЦДА). Координаты точек отрезка с концами (x0,y0) и (x1,y1), лежащего в плоскости R2, принимают значения
x=x0+t(x1-x0),
y=y0+t(y1-y0),
где 0 £ t £ 1 . Поэтому, выбрав достаточно малое число e > 0 и придавая координатам x и y приращения e×(x1-x0) и e×(y1-y0), мы могли бы строить точки отрезка, если бы дисплей обладал абсолютной точностью. Поскольку абсолютной точности нет, мы вынуждены использовать округления значений x и y , полученных после очередной пары приращений, с точностью до целых чисел.
Положим Dx=x1-x0, Dy=y1-y0. Так как округление произвольного вещественного числа r Î R равно целой части числа 0.5+r, с помощью данного алгоритма (при условии, что 1/e является целым положительным числом) генерируются точки, имеющие координаты
X=(int)(0.5+x0+e×i×Dx),
Y=(int)(0.5+y0+e×i×Dy),
где i пробегает значения i=0,1,…,1/e.
Для того чтобы каждый раз не делать округлений, заводятся два аккумулятора — один для дробной части числа x, другой – для дробной части числа y. Значения приращений, оба по модулю меньшие единицы, на каждом шаге прибавляются к дробным частям. Если один из аккумуляторов переполнился, в том смысле, что его значение стало больше или равно 1 (либо меньше 0), то от этого аккумулятора вычитается (либо прибавляется к аккумулятору, в зависимости от направления движения) единица, а значение соответствующей целочисленной координаты увеличивается (либо уменьшается) на единицу и ставится точка (X,Y). Вместо дробных частей в аккумуляторах следует хранить дробные части, умноженные на такое натуральное M, что K = e×M — целое число. В этом случае аккумуляторы получают приращения K×(x1-x0) и K×(y1-y0) , вместо e×(x1-x0) и e×(y1-y0). Поскольку
|e×(x1-x0)| £ 1, |e×(y1-y0) |£ 1,
содержимое каждого аккумулятора будет целым числом, лежащим в диапазоне от 0 до M-1. Последовательность генерируемых точек зависит от выбора числа e. Мы рассмотрим здесь два случая.
1) Симметричный ЦДА. Пусть n>0 — такое натуральное число, что при любых значениях (x0,y0), (x1,y1) координат пикселов выполнено неравенство
2n-1£max{|x1-x0|,|y1-y0|}<2 n. Полагая e=1/2n, получаем ЦДА, называемый симметричным. Для адаптеров CGA, EGA и VGA число n равно 10. Полагая M=1024, находим K=1. Начальные значения аккумуляторов равны 512. Аккумуляторы получают приращения x1-x0 и y1-y0. Если значение какого-нибудь аккумулятора стало меньше 0, либо больше или равно 1024, то соответствующая координата изменяется, к аккумулятору прибавляется приращение и ставится точка. Приходим к такой реализации алгоритма:
Программа
//Генерация точек отрезка методом симметричного ЦДА
#include <stdio.h>
#include <conio.h>
#include <graphics.h>
int x0, y0; //Координаты центра системы координат относит. лев. верх. угла
int hx=3, hy=3; //1/2 ширины и длины пиксела
//Функция определения знака целого числа
int sign (int r)
{
if (r>0) return 1;
else if (r<0) return -1;
else return 0;
}
//Вывод "крупного" пиксела на экран
void point( int ix, int iy )
{bar(x0+hx*2*ix-hx+1, y0-hy*2*iy-hy+1,x0+hx*2*ix+hx-1, y0-hy*2*iy+hy-1);}
//Генерация и вывод точек отрезка
void symcda(int x0, int y0, int x1, int y1)
{
int res_x=512, res_y=512; //Инициализация аккумуляторов
int x=x0, y=y0; //Начало отрезка
int dx=x1-x0, dy=y1-y0;
int ex=sign(dx), ey=sign(dy);
point (x,y); //Выводим первый пиксел
while (!(x==x1 && y==y1)) //Цикл пока не дойдем до конца отрезка
{
res_x+=dx;
//Проверка аккумулятора
if (res_x>=1024 || res_x <0)
{
x+=ex;
point(x,y);//Вывод очередного пиксела
res_x-=ex*1024;
}
res_y+=dy;
//Проверка аккумулятора
if (res_y>=1024 || res_y<0)
{
y+=ey;
point(x,y);//Вывод очередного пиксела
res_y-=ey*1024;
}
}
}
main()
{
int gdriver=DETECT, gmode;
initgraph (&gdriver, &gmode, "D:\BC\BGI");
x0=getmaxx()/2; y0=getmaxy()/2;
moveto(0,y0); linerel(getmaxx(),0);
moveto(x0,0); linerel(0, getmaxy());
symcda(0,0,5,3); //Вывод отрезка
getch(); //Ожидание нажатия клавиши
closegraph(); //Выключение графического режима
}
Будут выведены точки (рис. 1) (0,0), (1,0), (1,1), (2,1), …
>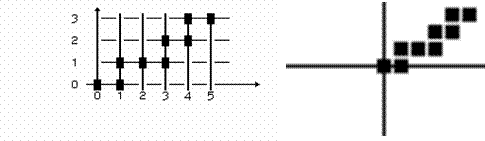
Рис. 1. Симметричный ЦДА
2) Простой ЦДА. В простом ЦДА e=1/max{|x1-x0|, |y1-y0|}. В этом случае либо e×(x1-x0), либо e×(y1-y0) по модулю равно 1, поэтому для хранения дробной части можно обойтись одним аккумулятором. Положим l=max{|x1-x0|, |y1-y0|}. Приращения по x и y будут равны dx=(x1-x0)/l и dy=(y1-y0)/l. Координаты точек, генерируемых простым ЦДА, будут принимать значения

Рис. 2. Простой ЦДА
X=(int)(0.5+x0+i×dx ),
Y=(int)(0.5+y0+i×dy ),
где i=0,1,…,l.
Программа
//Метод простого ЦДА
#include<conio.h>
#include<graphics.h>
#include<math.h>
int x0, y0; //Координаты центра системы координат относит. лев. верх. угла
int hx=3, hy=3; //1/2 ширины и длины пиксела
//Функция определения знака целого числа
sign(int r)
{
if(r>0) return 1;
else if(r<0) return -1;
else return 0;
}
//Вывод "крупного" пиксела на экран
void point(int ix, int iy)
{bar(x0+hx*2*ix-hx+1, y0-hy*2*iy-hy+1,x0+hx*2*ix+hx-1, y0-hy*2*iy+hy-1);}
//Генерация и вывод точек отрезка
void line_cda(int x0,int y0,int x1,int y1)
{
int i,l,x,y;
if(abs(x1-x0)>abs(y1-y0)) l=abs(x1-x0);
else l=abs(y1-y0);
if(l==0) {point(x0,y0); return;}
float hhx=1, hhy=1;
float dx=(float)((x1-x0)/float(l));
float dy=(float)((y1-y0)/float(l));
int ex=sign(x1-x0), ey=sign(y1-y0);
float rez=0.5; //аккумулятор
x=x0; y=y0;
int flagx=0, flagy=0; //флаги для проверки на конечную точку
do
{
if(abs(dx)<abs(dy))
{
//приращение всегда по у, а по х при условии rez<=0 rez>=1
point(x,y);
rez+=dx;
if(rez>=1||rez<=0)
{
x+=ex*hhx;
rez-=ex;
}
if(!flagx) flagx=x==x1?1:0;
y+=ey*hhy;
if(!flagy) flagy=y==y1?1:0;
}
else
{
//всегда по х, а по у при условии rez<=0 rez>=1
point(x,y);
x+=ex*hhx;
if(!flagx)flagx=x==x1?1:0;
rez+=dy;
if(rez>=1||rez<=0) {y+=ey*hhy; rez-=ey;}
if(!flagy)flagy=y==y1?1:0;
}
}
while(!(flagx==1 && flagy==1));
point(x1,y1); //последняя точка
}
main()
{
int gdriver=DETECT, gmode;
initgraph (&gdriver, &gmode, "D:\BC\BGI");
x0=getmaxx()/2; y0=getmaxy()/2;
moveto(0,y0); linerel(getmaxx(),0);
moveto(x0,0); linerel(0, getmaxy());
line_cda(0,0,5,3); //Вывод отрезка
getch(); //Ожидание нажатия клавиши
closegraph(); //Выключение графического режима
}
Результаты работы программы приведены на рис. 2.
Алгоритм Брезенхема. Положим Dx=x1-x0, Dy=y1-y0 . Пусть 0£Dy£Dx. При изменении координаты x на 1 координата y увеличивается на величину Dy/Dx. Пусть (x,y) — точка пересечения идеальной прямой, проходящей через точки (x0,y0) и (x1,y1), с прямой x=X, где (X,Y) — координаты текущей выведенной точки. Положим d=y-Y. Будем в цикле производить следующие действия: ставим точку и увеличиваем X на 1. При этом величине d придадим приращение Dy/Dx. Если число d вышло из диапазона
-1/2£d<1/2 , то надо координату Y увеличить на 1, а число d уменьшить на 1. Затем переходим к началу цикла. Цикл повторяется Dx+1 раз. Например, при Dx=4, Dy=1 величина d будет принимать значения 0, 1/4, -1/2, -1/4, 0, в этом случае при x0=y0=0 будет сгенерирована последовательность точек – (0,0), (1,0), (2,1), (3,1), (4,1).
Пусть point(x,y) — функция изображения точки. Вводя переменную
e=d-1/2,-1£e<0, приходим к такому алгоритму
X, Y, Dx, Dy — целые
e — вещественное
X = x0, Y = y0
Dx = x1-x0, Dy = y1 -y0(0£ Dy£ Dx)
e = -1/2
for i = 0 to Dx
point(X,Y)
X = X + 1
e = e + Dy/Dx
while (e³0)
Y=Y+1
e=e-1
end while
next i
finish
В отличие от стандартных вариантов, данная версия генерирует и последнюю точку (x1,y1). Полагая E=2×Dx×e, приходим к целочисленному алгоритму Брезенхема генерации точек отрезка (при условии 0£Dy£Dx):
X, Y, Dx, Dy, E — целые
X=x0, Y=y0
Dx = x1–x0, Dy = y1-y0
E = -Dx
for i = 0 to Dx
point(X,Y)
X = X + 1
E = E + 2×Dy
while(E ³ 0)
Y = Y + 1
E = E — 2*Dx
end while
next i
finish
Если (Dx,Dy) принадлежат не первой октанте, то точки (X,Y) генерируются симметрично. Подробнее, пусть x0, y0, x1, y1 — произвольные целые числа. Тогда, если |Dx|больше либо равно |Dy| , то вектор (Dx,Dy) находится в одной из октант I, IV, V, VIII. В этом случае координата X генерируемой точки получает на каждом шаге приращение sign(Dx). Если же |Dx|<|Dy|, то надо придавать приращение sign(Dy) координате Y. Приходим к окончательной версии алгоритма Брезенхема.
x0, y0, x1, y1 — входные параметры, целые
X, Y, dX, dY, E, sx, sy, temp, swap, i — целые
dX = |x1-x0|, dY = |y1-y0|
sx = sign(x1-x0) , sy = sign(y1-y0)
if dY > dX (если направление Y — главное)
temp = dX, dX=dY, dY=temp — переставить dX и dY
swab = 1 — была перестановка
else swab = 0
end if-else
E = -dX
for i = 0 to dX
point(X,Y)
E = E + 2?dY
while (E ? 0)
if (swab = 1) X = X + sx
else Y = Y + sy
end if-else
E = E – 2*dX
end while
if (swab = 1) Y = Y + sy
else X = X + sx
end if-else
next i
finish
Пример программной реализации алгоритма Брезенхема приводится также в пп. 2.2 (пример 2.1).
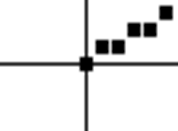
Рис. .3. Алгоритм Брезехема
Программа
//Метод Брезенхема
#include<conio.h>
#include<graphics.h>
#include<math.h>
int x0, y0; //Координаты центра системы координат относит. лев. верх. угла
int hx=3, hy=3; //1/2 ширины и длины пиксела
//Вывод "крупного" пиксела на экран
void point(int ix, int iy)
{bar(x0+hx*2*ix-hx+1, y0-hy*2*iy-hy+1,x0+hx*2*ix+hx-1, y0-hy*2*iy+hy-1);}
//Функция вывода отрезка по алгоритму Брезенхема
bresenham(int ix0, int iy0, int ix1, int iy1)
{
int ix, iy, delta_x, delta_y, esh, sx, sy;
int register temp, swab, i;
ix=ix0; iy=iy0;
delta_x=abs(ix1-ix0); delta_y=abs(iy1-iy0);
if (ix1-ix0>=0) sx=1; else sx=-1;
if (iy1-iy0>=0) sy=1; else sy=-1;
if (ix1==ix0) sx=0;
if (iy1==iy0) sy=0;
//Обмен значений delta_x delta_y в зависимости от угла
if (delta_y > delta_x)
{
temp=delta_x;
delta_x=delta_y;
delta_y=temp;
swab=1;
}
else swab=0;
//Инициализация Е с поправкой на половину пиксела
esh=2*delta_y-delta_x;
for(i=0;i<=delta_x;i++)
{
point(ix,iy);
while(esh>=0)
{
if (swab==1) ix=ix+sx; else iy=iy+sy;
esh=esh-2*delta_x;
}
if (swab==1)iy=iy+sy; else ix=ix+sx;
esh=esh+2*delta_y;
}
}
main()
{
int gdriver=DETECT, gmode;
initgraph (&gdriver, &gmode, "D:\BC\BGI");
x0=getmaxx()/2; y0=getmaxy()/2;
moveto(0,y0); linerel(getmaxx(),0); //Вывод осей координат
moveto(x0,0); linerel(0, getmaxy());
bresenham(0,0,5,3); //Вывод отрезка
getch(); //Ожидание нажатия клавиши
closegraph(); //Выключение графического режима
}
Результаты работы программы приведены на рис. 3.
Примечание. Для улучшения качества изображения применяются алгоритмы сглаживания лестничного эффекта. Точки, находящиеся дальше от прямой, выводятся с меньшей интенсивностью, чем те, которые находятся на прямой. В алгоритме Брезенхема в качестве меры удаленности может быть принят параметр E.
Метод приращений. В пп. 2.3 мы рассмотрим метод приращений для генерации точек кривой. Метод приращений также можно применить и для генерации точек прямой.
Запишем уравнение прямой, проходящей через точки (x0,y0) и (x1,y1), в виде f(x,y)=0, а именно: f(x,y)=Dy(x-x0) — Dx(y-y0) = 0, где Dx = x1-x0 и Dy=y1-y0. Все точки области, содержащей отрезок прямой f(x,y)=0, можно разбить на три множества: множество точек, принадлежащих прямой (для этих точек выполняется условие f(x,y)=0), множество точек, расположенных справа от прямой (для них выполнено условие f(x,y)>0), и множество точек, расположенных слева от прямой (для них выполнено условие f(x,y)<0). Основную идею метода приращений можно сформулировать следующим образом. Если мы выставили точку слева от прямой, то мы стремимся перейти на правую сторону от прямой и наоборот.
Сначала рассмотрим частный случай, когда отрезок прямой принадлежит первой октанте, а затем опишем алгоритм в общем случае и приведем текст программы.
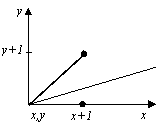
Рис. 4. Перемещения
Пусть отрезок прямой принадлежит первой октанте плоскости, т. е. Dx>0, Dy>0 и Dx>Dy. Начальная точка (x0,y0) принадлежит прямой, следовательно f(x0,y0)=0. Пусть мы сгенерировали некоторую точку (x,y), близкую к идеальной прямой. Так как отрезок принадлежит первой октанте, то из этой точки мы можем перейти либо в точку (x+1,y), либо в точку (x+1,y+1) (рис. 4). При этом f(x+1,y)>0, а f(x+1,y+1)<0. Следовательно, если f(x,y)<0, то переходим в точку (x+1,y), для которой f(x+1,y)>0, и наоборот, если f(x,y)?0, то переходим в точку (x+1,y+1), для которой f(x+1,y+1)<0.
Для уменьшения времени работы программы вычислим значения приращений delta1 и delta2:
delta1=f(x+1,y)–f(x,y)=Dy(x+1-x0)-Dx(y-y0)-Dy(x-x0)+Dx(y-y0)=Dy>0,
delta2=f(x+1,y+1)–f(x,y)=Dy(x+1-x0)-Dx(y+1-y0)-Dy(x-x0)+Dx(y-y0)=
Dy-Dx<0.
Приращение delta1 положительно, т.к. Dy>0, приращение delta2 отрицательно, т.к. Dx>0, Dy>0, Dx>Dy для первой октанты. Отметим, что независимо от того, в какую точку мы переходим (в (x+1,y) или в (x+1,y+1)), координата x увеличивается на единицу.
Запишем алгоритм:
x, y, Dx, Dy, delta, delta1, delta2 — целые
x = x0, y = y0 // начальная точка (x0, y0)
Dx = x1 – x0, Dy = y1 – y0
delta = 0, delta1 = Dy, delta2 = Dy — Dx
while (x ≠ x1 & y ≠ y1) // пока не придем в точку (x1, y1)
point (x,y) // ставим точку с координатами (x, y)
if (delta < 0)
delta = delta + delta1 // положительное приращение
else
delta = delta + delta2 // отрицательное приращение
y = y+1 // y увеличивается на 1
end if-else
x = x+1 // x увеличивается на 1
end while
Сформулируем алгоритм метода приращений для общего случая. Запишем уравнение прямой, проходящей через точки (x0,y0) и (x1,y1),
как f(x,y)=Dy(x-x0) — Dx(y-y0) = 0, где Dx = x1-x0 и Dy=y1-y0. Для всякой точки, лежащей справа от направленного отрезка, соединяющего точки (x0,y0) и (x1,y1), выполнено неравенство f(x,y)>0. Если точка (x,y) лежит слева, то f(x,y)<0. Алгоритм генерации точек методом приращений заключается в следующем. Сначала обрабатываются случаи, когда Dx=0, либо Dy=0, либо |Dx|=|Dy|. Затем, в предположении, что ни одно из этих условий не выполнено, выбираются два направления движения точки: первое направление параллельно одной из координатных осей и равно (sign(Dx),0), если |Dx|>|Dy|, и (0,sign(Dy)), если |Dx|<|Dy|; второе направление равно (sign(Dx),sign(Dy)). Если генерируемая точка перемещается во втором направлении, то функция f(x,y) получает приращение ¶2f(x,y)=(Dy)sign(Dx)-(Dx)sign(Dy), знак которого не зависит от точки (x,y). Если |Dx|>|Dy|, то при перемещении точки в первом направлении приращение будет равно ¶1f(x,y)=(Dy)sign(Dx). Если |Dx|<|Dy|, — то ¶1 f(x,y)=-(Dx)sign(Dy). Во всех случаях приращения ¶1f(x,y) и ¶2f(x,y) имеют противоположные знаки. Стало быть, если текущая точка находится справа от отрезка, то ее следует переместить в том направлении 1 или 2, при котором приращение функции f(x,y) отрицательно, а если слева, то выбирается оставшееся из двух направление. Рассмотрим пример реализации данного алгоритма:
Программа
#include <stdio.h>
#include <conio.h>
#include <graphics.h>
#include <math.h>
int x0, y0 , hx=3, hy=3;
//Функция определения знака целого числа
int sign (int r)
{
if (r>0) return 1;
else if (r<0) return -1;
else return 0;
}
//Функция вывода крупного пиксела
void point (int ix, int iy)
{bar(x0+hx*2*ix-hx+1, y0-hy*2*iy-hy+1, x0+hx*2*ix+hx-1, y0-hy*2*iy+hy-1);}
//Генерация точек прямой методом приращений
void line4 (int x0, int y0, int x1, int y1)
{
int x=x0, y=y0;
int dx=x1-x0, dy=y1-y0;
int delta=0, ex=sign(dx), ey=sign(dy);
point (x,y);
//Если dx = 0, то выводится вертикальный отрезок
if (dx==0)
{while (y!=y1) point (x, ++y); return;}
//Если dy = 0, то выводится горизонтальный отрезок
if (dy==0)
{while (x!=x1) point (++x, y); return;}
//Если abs(dx) = abs(dy):
if (abs(dx)==abs(dy))
{
while (x!=x1) {x+=ex; y+=ey; point(x,y);}
return;
}
//Основной цикл
while (!(x==x1 && y==y1))
{
if (delta<=0)
{
if (dy*ex-dx*ey>0)
{
x+=ex; y+=ey; delta+=dy*ex-dx*ey;
point(x,y);
}
else
if (abs(dx)>abs(dy))
{
x+=ex; delta+=dy*ex;
point(x,y) ;
}
else
{
y+=ey; delta -=dx*ey;
point(x,y);
}
}
else
{
if (dy*ex-dx*ey<0)
{
x+=ex; y+=ey; delta+=dy*ex-dx*ey;
point(x,y);
}
else
if (abs(dx)>abs(dy))
{
x+=ex; delta+=dy*ex;
point(x,y);
}
else
{
y+=ey; delta-=dx*ey;
point(x,y) ;
}
}
}
}
main()
{
int gdriver=DETECT, gmode;
initgraph(&gdriver, &gmode, "D:\BC\BGI");
x0=getmaxx()/2; y0=getmaxy()/2;
moveto(0,y0); linerel(getmaxx(),0);
moveto(x0,0); linerel(0, getmaxy());
line4(0,0,5,3);
getch();
closegraph();
}
Точки, выведенные на экран (рис. 5), отличаются от точек, генерируемых с помощью симметричного ЦДА.
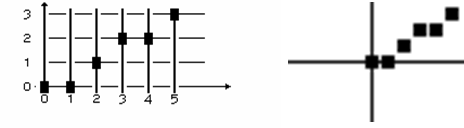 Рис. 5. Метод приращений
Рис. 5. Метод приращений
Метод приращений, использующий четыре перемещения.
Алгоритм генерации точек прямой по методу приращений можно модифицировать следующим образом: выбор двух направлений перемещения точки производится не из восьми возможных направлений, а из четырех. Разрешается выбирать одно из вертикальных и одно из горизонтальных направлений перемещения точки.
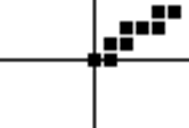
Рис. 6. Метод приращений, использующий четыре перемещения
Программа
//Метод приращений использующий четыре перемещения
#include<conio.h>
#include<graphics.h>
#include<math.h>
int x0, y0; //Координаты центра системы координат относит. лев. верх. угла
int hx=3, hy=3; //1/2 ширины и длины пиксела
//Вывод "крупного" пиксела на экран
void point(int ix, int iy)
{bar(x0+hx*2*ix-hx+1, y0-hy*2*iy-hy+1,x0+hx*2*ix+hx-1, y0-hy*2*iy+hy-1);}
//Функция вывода отрезка по методу
//приращений использующий четыре перемещения
line4(int x0, int y0, int x1, int y1)
{
int dx=abs(x1-x0), dy=abs(y1-y0);
int ex, ey;
if (x1>x0) ex=1; else ex=-1;
if (y1>y0) ey=1; else ey=-1;
int E=0, x=x0, y=y0;
while((y!=y1) || (x!=x1))
{
point(x,y);
if (E>0) {E-=dx; y+=ey;} else {E+=dy; x+=ex;}
}
point(x,y);
}
main()
{
int gdriver=DETECT, gmode;
initgraph (&gdriver, &gmode, "D:\BC\BGI");
x0=getmaxx()/2; y0=getmaxy()/2;
moveto(0,y0); linerel(getmaxx(),0); //Вывод осей координат
moveto(x0,0); linerel(0, getmaxy());
line4(0,0,5,3); //Вывод отрезка
getch(); //Ожидание нажатия клавиши
closegraph(); //Выключение графического режима
}
Результаты работы программы приведены на рис. 6.