Существуют три основные операции между логическими переменными конъюнкция (логическое умножение), дизъюнкция (логическое сложение) и инверсия (логическое отрицание). Операция инверсия обозначается чертой над логическим выражением. По аналогии с алгеброй чисел в алгебре логики используются следующие обозначения операций.
Конъюнкция: 
.
Дизъюнкция: 
.
Инверсия: 
.
Применительно к логическим операциям существуют теоремы:
Коммутативный закон: 
, 
.
Ассоциативный закон: 
, 
.
Дистрибутивный закон: 
, 
.
Правило склеивания: 
, 
.
Правило повторения: 
, 
.
Правило отрицания: 
, 
.
Правило двойного отрицания: 
.
Теорема де Моргана: 
, 
.
Операции с 0 и 1: 
, 
.
, 
.
, 
.
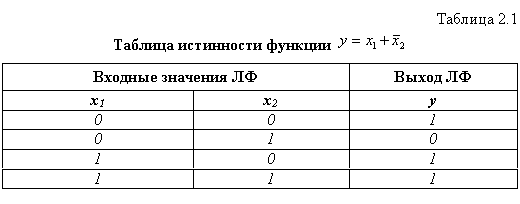
С помощью логических операций можно задать логическую функцию (ЛФ), например: 
. Значения логической функции для разных сочетаний значений входных переменных — или, как это иначе называют, наборов входных переменных — обычно задаются специальной таблицей. Такая таблица называется таблицей истинности (табл. 2.1).