Постановка задачи. Дано m предметов и n ящиков, в которые размещаются предметы. Сколько существует размещений, удовлетворяющих некоторым заданным условиям?

Определение 1

Размещением с повторениями называется функция:

f: {x₁, x₂, …, x_m} ®{y₁,y₂, …,y_n}.

Элементы x_i называются предметами, а y_j  — ящиками.

Полагая  a_i = f(x_i )_, легко  убедиться в том, что число всех размещений с повторениями равно количеству последовательностей {a₁,a₂, …, a_m}  чисел 1 £ a_i £ n  и, значит, оно равно n^m.

Определение 2

Рассмотрим некоторое конечное множество равновероятных элементарных событий, которые мы будем иногда назвать исходами. Событием называется подмножество множества всех исходов. Его элементы называются благоприятными исходами.  Вероятность события определяется как отношение количества благоприятных исходов к количеству всех исходов.

Например, если мы бросаем монету, то возможны два исхода. Число исходов выпадения «орла» равно 1. Значит, вероятность выпадения орла равно 0,5.

Упражнение 1

Бросают две игральные кости. Найти вероятность выпадения 10 очков.

Решение

Напомним, что игральная кость – это кубик, каждой грани которого соответствует одно число от 1 до 6. В данном случае число всех исходов равно 6². Благоприятные исходы: (4,6), (5,5), (6,4). Отсюда вероятность равна:

p = 3/36 = 1/12.

Определение 3

Размещением называется произвольная инъекция:

f: {x₁, x₂, …, x_m} ®{y₁,y₂, …,y_n}

(в каждый ящик размещают не более одного предмета).

Теорема 1

Число размещений равно:

.

Доказательство

Первый предмет можно разместить n способами, второй – n-1, …, m-й – n-m+1. Получаем:

.

Упражнение 2

В группе m студентов. Найти вероятность того, что найдется два студента, родившиеся в один день года.

Решение

Полагаем, что год не високосный. Число всех вариантов 365^m. Число неблагоприятных вариантов равно:

,

где n = 365.

Получаем:

.

Результаты вычислений  значений вероятности при различных m следующие:

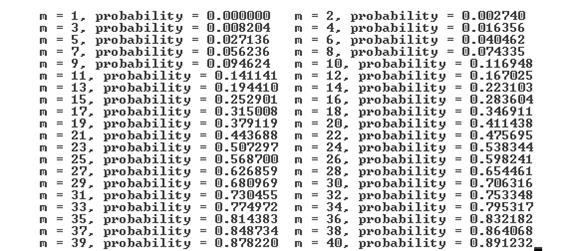
Например, если число студентов равно 23, то вероятность равна примерно 0.5.

Определение 4

Пусть заданы m ящиков. Упорядоченным размещением предметов a₁, a₂, …, a_n называется указание последовательности предметов для каждого ящика, при котором каждый предмет участвует ровно один раз.

Пример 1

На рисунке 2.1 показаны упорядоченные размещения предметов a, b по трем ящикам. Сначала размещается буква a в первый ящик и одним из четырех способов размещается буква b. Потом буква a размещается во второй ящик, в этом случае снова буква b размещается одним из четырех способов. Затем буква a размещается в третий ящик, буква b размещается одним из четырех способов. Всего получаем 12 упорядоченных размещений.

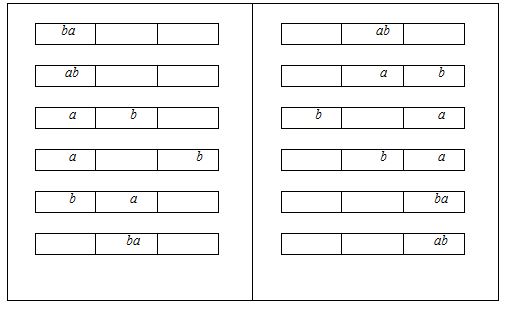
Рис. 2.1. Упорядоченные размещения

Теорема 2

Число  [m]n  упорядоченных размещений n предметов в m ящиков равно:

m(m + 1) … (m + n - 1).

Доказательство

После размещения  первого предмета в ящик одним из m способов

a1

∙ ∙ ∙

второй  предмет может быть размещен одним из m + 1 способов. Предположим, что уже размещено i-1 предметов, и пусть при k = 1, 2, …, m  в k-м  ящике находится  r_k  объектов. Тогда i-й объект может быть добавлен одним из

(r₁ + 1) + (r₂ + 1) + … + ( r_m +1) = i - 1 + m

способов.    

Отсюда  число всех упорядоченных размещений будет  равно:

m(m + 1) … (n - 1 + m).