Определение 2.2.2. Конечным автоматом (КА) называется следующая пятерка:

A = < V, Q, , q₀, F >,

где

V = {a₁, a₂, …, a_m} – входной алфавит (конечное множество символов);

Q = {q₀, q₁, …, q_n-1} – алфавит состояний (конечное множество символов );

: Q x V  Q – функция переходов;

q₀  Q – начальное состояние конечного автомата;

F  Q – множество заключительных состояний.

На содержательном уровне функционирование КА можно представить сле­дующим образом.

Имеется бесконечная лента, разбитая на ячейки, в каждой из которых мо­жет находиться один символ из V. На ленте записана цепочка  V*. Ячейки слева и справа от цепочки не заполнены. Имеется конечное устройство управ­ления (УУ) с читающей головкой, которое может последовательно считывать символы с ленты, передвигаясь вдоль ленты слева направо. При этом УУ мо­жет находиться в каком-либо одном состоянии из Q. Начинает свою работу УУ всегда в начальном состоянии q₀Q, а завершает в одном из заключительных состояний F  Q; Каждый раз, переходя к новой ячейке на ленте, УУ переходит в новое состояние в соответствии с функцией . Схематически конструкция КА показана  на рис. 2.1.

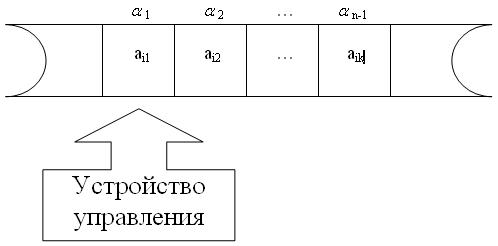
Рис. 2.1. Схема конечного автомата

Отображение δ (функцию переходов КА) можно представить различными способами. Основные из них:

· совокупность команд;

· диаграмма состояний;

· матрица переходов.

Команда конечного автомата записывается следующим образом:

(q_i, a_j) → q_k, где: q_i, q_k  Q; a_j  V.

Данная команда обозначает, что КА находится в состоянии q_i, читает с лен­ты символ а_j и переходит в состояние q_k.

Графически команда представляется в виде дуги графа, идущей из вер­шины q_i в вершину q_k и помеченной символом а_j входного алфавита:

Графическое представление всего отображения  называют диаграммой со­стояний конечного автомата. Диаграмма состояний в этом случае — это ори­ентированный граф, вершинам которого поставлены в соответствие символы из множества состояний Q, а дугам — команды отображения .

Если КА оказывается в ситуации (q_i­­, а_j), которая не является левой частью какой-либо команды, то он останавливается. Если же УУ считает все символы цепочки , записанной на ленте, и при этом перейдет в заключительное состоя­ние q_iF, то говорят, что цепочка допускается конечным автоматом.

Матрица переходов КА строится следующим образом: столбцы матрицы соответствуют символам из входного алфавита, строки — символам из алфа­вита состояний, а элементы матрицы соответствуют состояниям, в которые переходит КА для данной комбинации входного символа и символа состояния.