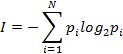Как уже отмечалось, понятие информации можно рассматривать при различных ограничениях, накладываемых на ее свойства, т.е. при различных уровнях рассмотрения. В основном выделяют три уровня – синтаксический, семантический и прагматический. Соответственно на каждом из них для определения количества информации применяют различные оценки.

На синтаксическом уровне для оценки количества информации используют вероятностные методы, которые принимают во внимание только вероятностные свойства информации и не учитывают другие (смысловое содержание, полезность, актуальность и т.д.). Разработанные в середине XXв. математические и, в частности, вероятностные методы позволили сформировать подход к оценке количества информации как к мере уменьшения неопределенности знаний.

Такой подход, называемый также вероятностным, постулирует принцип: если некоторое сообщение приводит к уменьшению неопределенности наших знаний, то можно утверждать, что такое сообщение содержит информацию. При этом сообщения содержат информацию о каких-либо событиях, которые могут реализоваться с различными вероятностями.

Формулу для определения количества информации для событий с различными вероятностями и получаемых от дискретного источника информации предложил американский ученый К. Шеннон в 1948г. Согласно этой формуле количество информации может быть определено следующим образом:

, где I – количество информации; N – количество возможных событий (сообщений); p_i – вероятность отдельных событий (сообщений).

Определяемое с помощью формулы (2.1) количество информации принимает только положительное значение. Поскольку вероятность отдельных событий меньше единицы, то соответственно выражение log₂,- является отрицательной величиной и для получения положительного значения количества информации в формуле (2.1) перед знаком суммы стоит знак «минус».

Если вероятность появления отдельных событий одинаковая и они образуют полную группу событий, т. е.:

,

то формула (2.1) преобразуется в формулу Р. Хартли:

В формулах (2.1) и (2.2) отношение между количеством информации  I и соответственно вероятностью (или количеством) отдельных событий выражается с помощью логарифма.

Применение логарифмов в формулах (2.1) и (2.2) можно объяснить следующим образом. Для простоты рассуждений воспользуемся соотношением (2.2). Будем последовательно присваивать аргументу N значения, выбираемые, например, из ряда чисел: 1, 2, 4, 8, 16, 32, 64 и т.д. Чтобы определить, какое событие из N равновероятных событий произошло, для каждого числа ряда необходимо последовательно производить операции выбора из двух возможных событий.

Так, при N = 1 количество операций будет равно 0 (вероятность события равна 1), при N = 2, количество операций будет равно 1, при N = 4 количество операций будет равно 2, при N = 8, количество операций будет равно 3 и т.д. Таким образом, получим следующий ряд чисел: 0, 1, 2, 3, 4, 5, 6 и т.д., который можно считать соответствующим значениям функции I в соотношении (2.2).

Последовательность значений чисел, которые принимает аргумент N, представляет собой ряд, известный в математике как ряд чисел, образующих геометрическую прогрессию, а последовательность значений чисел, которые принимает функция I, будет являться рядом, образующим арифметическую прогрессию. Таким образом, логарифм в формулах (2.1) и (2.2) устанавливает соотношение между рядами, представляющими геометрическую и арифметическую прогрессии, что достаточно хорошо известно в математике.

Для количественного определения (оценки) любой физической величины необходимо определить единицу измерения, которая в теории измерений носит название меры. Как уже отмечалось, информацию перед обработкой, передачей и хранением необходимо подвергнуть кодированию.

Кодирование производится с помощью специальных алфавитов (знаковых систем). В информатике, изучающей процессы получения, обработки, передачи и хранения информации с помощью вычислительных (компьютерных) систем, в основном используется двоичное кодирование, при котором используется знаковая система, состоящая из двух символов 0 и 1. По этой причине в формулах (2.1) и (2.2) в качестве основания логарифма используется цифра 2.

Исходя из вероятностного подхода к определению количества информации эти два символа двоичной знаковой системы можно рассматривать как два различных возможных события, поэтому за единицу количества информации принято такое количество информации, которое содержит сообщение, уменьшающее неопределенность знания в два раза (до получения событий их вероятность равна 0,5, после получения – 1, неопределенность уменьшается соответственно: 1/0,5 = 2, т.е. в2 раза). Такая единица измерения информации называется битом (от англ. слова binary digit – двоичная цифра). Таким образом, в качестве меры для оценки количества информации на синтаксическом уровне, при условии двоичного кодирования, принят один бит.

Следующей по величине единицей измерения количества информации является байт, представляющий собой последовательность, составленную из восьми бит, т.е.:

1 байт = 2³ бит = 8 бит.

В информатике также широко используются кратные байту единицы измерения количества информации, однако в отличие от метрической системы мер, где в качестве множителей кратных единиц применяют коэффициент 10n, где n = 3, 6, 9 и т.д., в кратных единицах измерения количества информации используется коэффициент 2n. Выбор этот объясняется тем, что компьютер в основном оперирует числами не в десятичной, а в двоичной системе счисления.

Кратные байту единицы измерения количества информации вводятся следующим образом:

1 килобайт (Кбайт) = 210 байт = 1024 байт;

1 мегабайт (Мбайт) = 210 Кбайт = 1024 Кбайт;

1 гигабайт (Гбайт) = 210 Мбайт = 1024 Мбайт;

1 терабайт (Тбайт) = 210 Гбайт = 1024 Гбайт;

1 петабайт (Пбайт) = 210 Тбайт = 1024 Тбайт;

1 экзабайт (Эбайт) = 210 Пбайт = 1024 Пбайт.

Единицы измерения количества информации, в названии которых есть приставки «кило», «мега» и т.д., с точки зрения теории измерений не являются корректными, поскольку эти приставки используются в метрической системе мер, в которой в качестве множителей кратных единиц используется коэффициент 10ⁿ, где n = 3, 6, 9 и т.д. Для устранения этой некорректности международная организация International Electrotechnical Commission, занимающаяся созданием стандартов для отрасли электронных технологий, утвердила ряд новых приставок для единиц измерения количества информации: киби (kibi), меби (mebi), гиби (gibi), теби (tebi), пети (peti), эксби (exbi). Однако пока используются старые обозначения единиц измерения количества информации, и требуется время, чтобы новые названия начали широко применяться.

Вероятностный подход используется и при определении количества информации, представленной с помощью знаковых систем. Если рассматривать символы алфавита как множество возможных сообщений N, то количество информации, которое несет один знак алфавита, можно определить по формуле (2.1). При равновероятном появлении каждого знака алфавита в тексте сообщения для определения количества информации можно воспользоваться формулой (2.2).

Количество информации, которое несет один знак алфавита, тем больше, чем больше знаков входит в этот алфавит. Количество знаков, входящих в алфавит, называется мощностью алфавита. Количество информации (информационный объем), содержащееся в сообщении, закодированном с помощью знаковой системы и содержащем определенное количество знаков (символов), определяется с помощью формулы:

где V – информационный объем сообщения; I = log₂N, информационный объем одного символа (знака); К – количество символов (знаков) в сообщении; N – мощность алфавита (количество знаков в алфавите).