Как было указано ранее, КА является хорошей математической моделью для представления алгоритмов распознавания лексем в ЛА, в особенности для лексем из бесконечных классов. При этом источником, по которому строится КА, является регулярная грамматика.

Пусть задана регулярная грамматика G = <N, Т, Р, S>, правила которой име­ют вид:

А_i  а_j А_k или А_i  а_j., где А_i, А_k N и а_j Т.

Тогда конечный автомат А = <V, Q, , q₀, F>, допускающий тот же самый язык, что порождает регулярная грамматика G, строится следующим образом:

1) V = T;

2) Q =  N  {Z}, Z  N, Z  T, Z – заключительное состояние КА;

3) q₀ =  {S};

4) F = {Z};

5) отображение  строится в виде:

а) каждому правилу подстановки в грамматике G вида А_i  а_jА_k ставится в соответствие команда (A_i, a_j)  A_k;

б) каждому правилу  подстановки вида А_i  а_j ставится в соответствие команда (A_i, a_j)  Z.

Пример 2.2.2. Построить КА для грамматики из примера 2.2.1. Имеем А=<V,Q,, q₀, F>,

1) где V = T = {б, ц}

2) Q =  N  {Z} =  {I, K, Z}

3) q₀ =  {S} = {I}

4) F = {Z}

1) :

a) в виде совокупности команд:

(I, б)  Z

(I, б)  К

(К, б)  К

(К, ц)  К

(К, б)  Z

(К, ц)  Z

б)  в виде диаграммы состояний (рис. 2.2)

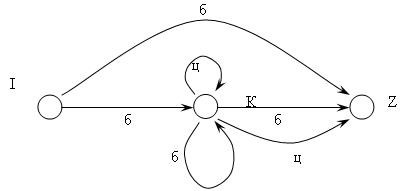
Рис. 2.2. Диаграмма состояний КА для идентификаторов

Допустим и обратный переход. Так конечному автомату А = <V, Q, , q₀, F> можно поставить в соответствие регулярную грамматику G = <N, Т, Р, S>, у которой:

1) T = V;

2) N =  Q;

3) S =  {q₀};

4) множество правил подстановки Р строится следующим образом:

каждой команде автомата (q_i,а_j)q_k ставится в соответствие правило подстановки q_i  a_jq_k, если q_k  Q, либо еще одно правило q_i  а_j, если q_k  F.