Различают детерминированные и недетерминированные конечные автома­ты. КА называется недетерминированным  (НДКА), если в диаграмме его состояний из одной вершины исходит несколько дуг с одинаковыми пометка­ми. Например, КА из примера 2.2.2 является НДКА. Хотя НДКА располагает, на первый взгляд, большими возможностями, чем детерминированный КА, клас­сы языков, которые они допускают, в действительности совпадают.

По описанию НДКА всегда можно построить описание детерминированного КА (ДКА). При этом НДКА А

1) с входным алфавитом V,

2) множеством состояний Q = {q₀,q,, …,q_n.,}

3) и функцией переходов  

преобразуется в ДКА А’, у которого:

1) V’ = V;

2) q₀‘ = {q₀};

3) Q’ = {, {q₀}, {q₁}, …, {q₀,…, q_n-1}};

1) ‘(q’, a) =

1) Заключительные состояния F’ — все подмножества Q, содержащие хотя бы одно заключительное состояние автомата А.

Пример 2.2.3. Пусть регулярный язык порождается грамматикой G = <N, Т, Р, S>, у которой N = {S, R}, Т = {a, b}, S = {S},

P = {S  aS | aR

        R  bR | a}

Построим НДКА А = <V, Q, , q_Q, F>. Имеем

1) V = Т = {a, b};

2) Q = {S, R, Z};

3) F = {Z}, отображение представлено на рис.2.3 в виде диаграммы состояний.

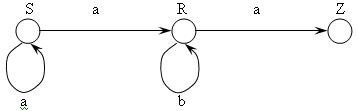
Рис 2.3. Диаграмма состояний НДКА из примера 2.2.3

Построим эквивалентный ему ДКА А’ = <V, Q’, ‘, q₀‘, F’>.

Возможно создание нескольких вариантов ДКА, распознающих язык L'(G’).

В первом случае компонента­ми ДКА будут:

V’ = V={a,b};

Q’ = {{S}, {R}, {S, R, Z}}; остальные 4 состояния можно отбросить, так как ни в одно из них автомат попасть не может;

q₀‘={S};

F’={{S,R,Z}};

функцию переходов ‘ можно задать с помощью следующих команд:

({S}, a)              {S, R, Z};

({S, R, Z}, a)     {S, R, Z};

({S, R, Z}, b)     {R};

({R}, b)             {R};

({R}, a)             {S, R, Z}.

Представление ‘ показано как в виде диаграммы состояний (рис 2.4), так и в виде матрицы переходов:

	a	b
S	S,R,Z
R	S,R,Z	R
S,R,Z	S,R,Z	R

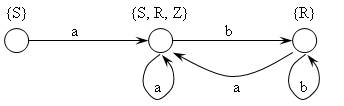
Рис 2.4. Диаграмма состояний ДКА

Построим по описанию ДКА А’ регулярную грамматику G’ = <N’ , Т’ , Р’, S’>. Для этого дадим новые обозначения элементам множества Q’ :

{S} — S’, {R} — R’, {S, R, Z} — К’.

Имеем N’ = {S’, R’, К’ }, T = {a, b}, S’ = {S’},

Р’ = {S’  аК’

         K’  aK’ | bR’ | a

         R’  bR’ | aK’ | a}.

Во втором случае компонента­ми ДКА будут:

V’ = V={a,b};

Q’ = {{S}, {R}, {S, R}, {Z}};

q₀‘ = {S};

F’ = {{S, R}, {Z}};

функцию переходов ‘ можно задать с помощью следующих команд:

({S}, a)              {S, R};

({S, R}, a)         {S, R};

({S, R}, b)         {R};

({R}, b)             {R};

({R}, a)             {Z}.

диаграмма состояний для этого варианта приведена на рис. 2.5.

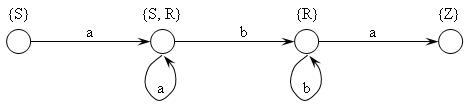
Рис 2.5. Диаграмма состояний ДКА

Для практических целей необходимо, чтобы конечный распознаватель иг­рал более активную роль и сам определял момент окончания входной последо­вательности символов с выдачей сообщения о правильности или ошибочности входной цепочки. Для этих целей входная цепочка считается ограниченной спра­ва концевым маркером ├.  Тогда для конечного автомата из примера 2.2.2 получаем:

V’=V U {├}.

А в диаграмму состояний КА вводятся интерпретиро­ванные состояния, будем обозначать эти состояния соответственно:

Z — «допустить входную цепочку»,

О — «запомнена ошибка во входной цепочке»,

Е — «отвергнуть входную цепочку».

Состояния Z и Е являются заключитель­ными, и в них КА переходит при прочтении концевого маркера  соответственно после обработки правильной или ошибочной входной цепочки. Состояние О является промежуточным, в него КА переходит из любого допустимого состо­яния КА при обнаружении ошибки во входной цепочке и остается в нем до поступления концевого маркера ├, после чего осуществляется переход в со­стояние Е — «отвергнуть входную цепочку».

Ниже приведена модифицированная диаграмма состояний конеч­ного распознавателя из примера 2.2.2 (рис. 2.6)

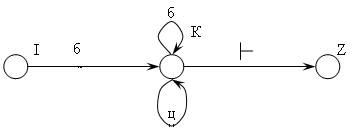
Рис. 2.6. Модифицированная диаграмма состояний КА для распознавания идентификаторов ( — не буква)

ц

Этой диаграмме состояний соответствует матрица переходов:

		0	1	2
		б	ц	-
0	I	K=1	E=3	E=3
1	K	K=1	K=1	Z=2

2-успех; 3-ошибка

Для данной матрицы переходов предполагается, что множества ц и  не пересекаются.